V1: A Visual Query Language for Property Graphs

Copyright © 2017-2023 Lior Kogan (koganlior1 [at] gmail [dot] com)

The “V1” name is a trademark of Lior Kogan.

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Commercial licenses and software tools are also available from Lior Kogan.

---

This page contains the description and the specifications of the V1 language. This content is periodically released in arXiv.

V1 is named after the primary visual cortex in our brain, which is also known as visual area one (V1).

V1 is dedicated to my ancestors all the way back and their descendants all the way forth.

Feedback, questions, corrections, and suggestions are welcome.

---

Table of Contents

• Introduction
• The Property Graph Data Model
• The Property Graph Schema
• Patterns and Pattern Languages
• A Song of Ice and Fire
• V1 Basics
• Expressions and Expression Constraints
• Data Types, Operators, and Functions
• Quantifiers
• Entity-Tags
• Negator
• Relationship/Path-Negator
• Combiner
• Chains, Horizontal Quantifiers, and Horizontal Combiner
• Latent Pattern-Entities
• Optional Components
• Untyped Entities
• Entity Type-Tags
• Untyped Relationships
• Relationship Type-Tags
• Null Entities
• Paths
• Shortest Paths
• Path Patterns
• Referencing Expression-Tags
• Aggregators
  • A1 Aggregator
  • A2 Aggregator
  • A3 Aggregator
• Min/Max Aggregators
  • M1 Aggregator
  • M2 Aggregator
  • M3 Aggregator
  • R1 Aggregator
• Aggregator Chains
• Aggregator Sequences
• Extended Aggregators
  • Extended A1 Aggregator
  • Extended A2 Aggregator
  • Extended A3 Aggregator
  • Extended M1 Aggregator
  • Extended M2 Aggregator
  • Extended M3 Aggregator
  • Extended R1 Aggregator
• Multivalued Functions and Expressions
• Application: Spatiotemporality

Introduction

The property graph is an increasingly popular data model. Pattern construction and pattern matching are important tasks when dealing with property graphs. Given a property graph schema 𝑆, a property graph 𝐺 conforming to 𝑆, and a query pattern 𝑃 conforming to 𝑆, all expressed in language 𝐿 = (𝐿_𝑆, 𝐿_𝐺, 𝐿_𝑃, 𝐿_𝑅), pattern matching is the process of finding, transforming, merging, and annotating subgraphs of 𝐺 that match 𝑃. The syntaxes of sublanguages 𝐿_𝑆, 𝐿_𝐺, 𝐿_𝑃, and 𝐿_𝑅 define what and how symbols can be combined to form well-formed schemas, graphs, patterns, and query results, respectively. A semantics of 𝐿_𝑃 is a mapping (𝑆, 𝐺, 𝑃) → 𝑅: which subgraphs of 𝐺 match 𝑃 and how to transform, merge, and annotate them. Expressive pattern languages support topological constraints, property value constraints, negations, quantifications, aggregations, and path semantics. Calculated properties may be defined for vertices, edges, and subgraphs, and constraints may be imposed on their evaluation result.

Many query posers are professionals (e.g., researchers, analysts, or investigators) who construct patterns as part of their daily work (e.g., investigative analytics). Such domain experts would like to construct patterns with minimal effort, minimal trial and error, and in a manner that is coherent with the way they think. The ability to express patterns in a way that is aligned with their mental processes is crucial to the flow of their work and to the quality of the insights they can draw. Many domain experts will not use textual property graph query languages (e.g., Gremlin, GSQL, Cypher, PGQL, G-CORE, and the proposed GQL) either because it can be too hard for someone with little or no programming or scripting skills, or because it requires them to spend too much time on the technicalities and distracts them from their line of inquiry. As a result, they are forced to use only a predefined set of query templates or work in concert with technical experts. Both solutions are far from satisfying.

Since the capabilities of the human visual system with respect to pattern perception are remarkable, it is a matter of course that query patterns were to be expressed visually. Indeed, five of the abovementioned languages use ‘ASCII art syntax’ for expressing topological constraints. Needless to say, this type of ‘visualization’ is quite limited. While the use of ASCII art declined during the 1990s in favor of graphical images, query languages began to adopt ASCII art only recently. Visual (graphical, diagrammatic) query languages have the potential to be much more ‘user-friendly’ than their textual counterparts in the sense that patterns may be constructed and understood much more quickly and with much less mental effort. Given a schema, interactive tools can allow query posers to construct valid patterns with minimal typing. A long-standing challenge is to design a visual query language that is generic, has rich expressive power, and is highly receptive and productive. V1 attempts to answer this challenge.

V1 is a declarative visual pattern query language for schema-based property graphs. V1 supports property graphs with mixed (both directed and undirected) edges, multivalued and composite properties, and null property values. V1 supports temporal data types, operators, and functions and can be extended to support additional data types, operators, and functions (one spatiotemporal model is presented). V1 is generic, concise, has rich expressive power, and is highly receptive and productive.

The Property Graph Data Model

The term property graph refers to both a mathematical structure and a data model; both are described below.

Mathematical Structure:

A graph is an ordered quintet 𝐺 = (𝑉, 𝐸, 𝐴, ψₑ, ψₐ) consisting of three pairwise disjoint sets and two functions. 𝑉 is a nonempty set whose elements are called vertices (nodes, dots, points), 𝐸 is a set whose elements are called undirected edges (undirected links, undirected lines), 𝐴 is a set whose elements are called directed edges (directed links, directed lines, arcs, arrows), ψₑ: E → { {u,v}: u,v ∈ V } is a total function mapping each undirected edge to an unordered pair of vertices, and ψₐ: A → { (u,v): u,v ∈ V } is a total function mapping each directed edge to an ordered pair of vertices. An undirected graph is a graph in which 𝐴 ≔ ∅. A directed graph (digraph, oriented graph) is a graph in which 𝐸 ≔ ∅. A mixed graph is a graph where both directed and undirected edges may exist.

Given undirected edge 𝑒 such that ψₑ(𝑒) = {𝑢,𝑣}, we say that 𝑒 is an edge between 𝑢 and 𝑣, 𝑒 connects (joins) 𝑢 and 𝑣, and 𝑢 and 𝑣 are adjacent. Likewise, given directed edge 𝑎 such that ψₐ(𝑎) = (𝑢,𝑣), we say that 𝑎 is an edge from 𝑢 to 𝑣, 𝑎 connects (joins) 𝑢 to 𝑣, 𝑣 is adjacent from (out-adjacent to) 𝑢, 𝑢 is adjacent to (in-adjacent to) 𝑣, 𝑢 is the tail (source vertex, initial vertex) of 𝑎, and 𝑣 is the head (target vertex, terminal vertex) of 𝑎. A loop is a directed or undirected edge connecting a vertex with itself. Multiple edges (parallel edges) are two or more undirected edges connecting the same unordered pair of vertices or directed edges connecting the same ordered pair of vertices. A simple graph is a graph in which multiple edges and loops are not allowed. A pseudograph is a graph in which multiple edges and loops are allowed.

An attributed graph is a generic term referring to graphs in which an attribute (single-attributed graph) or a set, a bag, or a list of attributes (multi-attributed graph) may be associated with each vertex (vertex-attributed graph), edge (edge-attributed graph), or the graph itself. An attribute may be a nominal value, an ordinal value, a key-value pair, or other annotation. (The term attributes is sometimes used to refer only to key-value pairs, while labels is used to refer to nominal attributes).

A property graph (PG, labeled property graph, LPG) is a vertex-multi-attributed edge-multi-attributed directed pseudograph in which:

• Each vertex has an attribute called label (vertex-labeled graph). Similarly, each edge has an attribute called label (edge-labeled graph). The set of vertex labels and the set of edge labels are disjoint.

• Each vertex, as well as each edge, has a set of attributes called properties. Each property is an ordered pair: the property’s name and the property’s value. For each vertex, as well as for each edge, the property names are pairwise distinct.

A mixed property graph is mixed instead of directed.

Data Model:

Data is a representation of information. A data element (i.e., datum) is an atomic unit of data, hence, an atomic unit of representation of information about the domain of discourse. A data model specifies the semantics and defines the structure of data elements and the relations between data elements. A data model consists of:

• A set of ontological concepts (e.g., entity, relationship, type, feature). The concepts are used for defining data elements and their relations. Usually, they are general, domain-agnostic, and are explained rather than defined.

• A structure (e.g., mathematical, diagrammatic) for organizing data elements.

The [mixed] property graph data model comprises the following concepts:

• An entity is a physical, conceptual, virtual, or fictional particular (e.g., a certain person, guild, or dragon).

• Each entity has a single type (e.g., Person)

• A (binary) relationship is an association or an interaction between a pair of entities or between an entity and itself. Each relationship is either directional (unidirectional, asymmetric) (e.g., an owns relationship between a Person entity and a Horse entity, an offspring relationship between two Person entities) or bidirectional (non-directional, symmetric, reciprocal) (e.g., a friend of relationship between two Person entities). Bidirectional relationships are supported only in the mixed property graph data model.

• Each relationship has a single type (e.g., owns)

• An action is an action of an entity (e.g., erupts for a Volcano entity) or an action on an entity (e.g., accused for a Person entity), when no other [known or relevant] entities are concerned. An action may also represent a state of an entity (e.g., sleeps action for a Person entity) or a state-change (e.g., falls asleep for a Person entity). Like relationships, actions are either directional or bidirectional. Bidirectional actions are supported only in the mixed property graph data model.

• Each action has a single type (e.g., erupts)

• Each entity, relationship, or action has a set of features (characteristics). Each feature has a name (e.g., birth date for a Person entity, timeframe for an owns association, timeframe for a sleeps action) and a value, for example, weight= 450. For each entity, relationship, or action, the feature names are pairwise distinct.

A property graph is hence a heterogeneous graph; it may contain entities of multiple types (multi-modal graph), relationships of multiple types (multi-relational graph), and, optionally, actions of multiple types. In addition, each entity, relationship, or action may have multiple features (multifeatured graph).

Types can be assigned based on many universals (qualities), e.g., person entities, red entities, owner entities. Usually, entities of the same type are semantically homogeneous. The same is true also for relationships and for actions. For property graphs, semantic homogeneity means:

• Repetition of existence: there are multiple entities of the same type, multiple relationships of the same type, and multiple actions of the same type.
• Repetition of features: entities of the same type have features of the same types. The same is true also for relationships and for actions.
• Repetitions of actions: entities of the same type ‘have’ actions of the same types.
• Repetition of relationships: pairs of entities of the same pair of entity-types have relationships of the same types.
• Type constancy: an entity’s type, a relationship’s type, and an action’s type do not change over time.

The property graph data model is a metamodel, as it does not specify types of entities, relationships, and actions, nor does it specify sets of features. It is domain-agnostic. Instead, domain-specific concepts may be specified and enforced using a property graph schema (see next section).

The [mixed] property graph data model comprises the following structure:

• All data elements are organized in a single [mixed] property graph mathematical structure.
• A null vertex is a propertyless vertex with a null label. Each null vertex is connected to exactly one edge. An edge connecting two null vertices is not allowed.
• Any vertex, except null vertices, represents an entity. The vertex’s label is an integer or a nonempty string identifying the entity’s type (e.g., Person, Guild, Dragon).
• An undirected edge {𝑢, 𝑣}, where both 𝑢 and 𝑣 are not null vertices, represents a bidirectional relationship between the entity represented by 𝑢 and the entity represented by 𝑣.
• A directed edge (𝑢, 𝑣), where both 𝑢 and 𝑣 are not null vertices, represents a directional relationship between the entity represented by 𝑢 and the entity represented by 𝑣.

• An edge, where one vertex is a null vertex, represents either

  • an entity’s action (e.g., sleeps action for a Person entity), or
  • a relationship between an entity and a nonspecific entity. Sometimes, an entity is unknown or unimportant, but the existence of a relationship and the values of the relationship’s properties - are important. For example, we may know that a given horse had different owners at different timeframes, but we do not know or care who owned it. Still, we want to be able to model such data.
• The edge’s label is an integer or a nonempty string identifying the relationship’s type (e.g., owns, member of) or the action’s type (e.g., sleeps).
• A directed graph edge represents a directional relationship or action, while an undirected edge represents a bidirectional relationship or action.
• Properties and subproperties represent features and subfeatures of entities (e.g., name property and first name subproperty for a Person entity), relationships (e.g., timeframe property for an owns association), and actions (e.g., timeframe for a sleeps action). For each entity, relationship, and action, property names are pairwise distinct strings or integers, each identifying the feature’s name, and each property value represents the feature’s value.

• Each feature value is represented using one of the property data types supported by the model. There is, however, no standard definition of which data types the model should support. In this paper, we will use the following:

  • The model defines a set of basic data types (e.g., string, integer, float).
  • A multivalue is a set, a bag, or a list of values. All values are of the same basic data type (e.g., each value is a string), the same multivalue type (e.g., each value is a set(string)), or the same composite type (e.g., each value is a {first: string, last: string} composite).
  • A multivalue type is defined by the collection type (set, bag, or list) and the data type of its elements. The definition must be nonrecursive.
  • A map is a set of (name, value) pairs in which the names are pairwise distinct strings or integers identifying the subfeatures names, and the values are the respective subfeature values.
  • A map type is defined by a set of (name, data type) pairs. The definition must be nonrecursive. A composite is a map in which each value is of a basic data type, a multivalue type, or a composite type.

  A basic property is a property whose value is of a basic data type. A multivalued property is a property whose value is a multivalue (e.g., set, bag, or list), e.g., titles: set(string) = {“Her Majesty”, “Her Royal Highness”}. A composite property is a property whose value is composite, e.g., name: (first: string, last: string) = (“Brandon”, “Stark”). Each member of a composite property is called a subproperty.

• null is a valid value for each nullable property and subproperty, regardless of its data type. Null-valued [sub]property indicates that a [sub]feature value is not specified.

  Several different interpretations can be associated with a null value. Following the terminology introduced by Codd and adopted by many authors, a null value is either

  • Applicable missing – at present, a value is applicable (applies to the particular entity, relationship, or action) but unknown (whatever the reason, the graph does not have the value). E.g., the temperature 1000 years ago today; the phone number of a person who owns a phone, but the number is unknown; an answer to a question – when the questionee refused to answer.
  • Inapplicable - at present, no value is applicable. E.g., the temperature tomorrow, previous citizenship when there is none, direct manager of the CEO, new hire’s not-yet-assigned employee ID, a phone number of a person who does not own a phone, an answer to a question – when the question was not posed to the questionee.

  Zaniolo proposed a third basic interpretation of null values:

  • No information – at present, the applicability of the unspecified value is unknown. E.g., a person’s phone number – when it is unknown whether the person owns a phone; an answer to a question – when it is unknown if the question was posed to the questionee.

  Codd, Zaniolo, and many others proposed using two or more types of null instead of a ‘generic’ null, but this approach remains mainly theoretical. In practice, null values often have no consistent semantics. For a birth date property, a null value would likely represent an unknown birth date, but for a death date property, a null value may represent that the date on which the person died is unknown (applicable missing), that the person is still alive (inapplicable), or that it is unknown if the person is still alive (no information).

  Though the semantic of null values is not always defined as part of the data model, nor as part of the data schema, it still must be well-defined for query languages’ operators and functions. E.g., what is the result of (yesterday’s date < person’s death date) when the death date is null? Often, null values represent applicable missing and no information, while magic values (e.g., “9999-12-31” for dates) represent inapplicable values. In addition, a sorting comparison operator is usually well-defined for null values and may differ from the standard comparison operator (e.g., should The five persons with the earliest birth date returns persons with a null birth date?)

• Should new information prove that two or more vertices represent the same entity, these vertices should be merged. Similarly, should new information prove that two or more edges represent the same relationship or action, these edges should be merged.

• Should new information prove that a vertex represents two or more entities, this vertex should be split. Similarly, should new information prove that an edge represents two or more relationships or actions, this edge should be split.

• Any pair of vertices, except null vertices, must be distinguishable, which means that vertices’ identifiers must be pairwise distinct, or there should be no pair of vertices with identical type, property values, and relationships. Similarly, any pair of edges must be distinguishable, which means that edges’ identifiers must be pairwise distinct, or there should be no pair of edges with identical type and property values that connect the same pair of vertices or the same vertex and a null vertex. An identifier is a set of properties (often just an automatically generated index) that collectively uniquely identifies the element.

𝑛-ary relationships, where 𝑛 > 2, are not supported. However, this poses no expressivity limitation since any 𝑛-ary relationship, 𝑛 > 2, can be reframed as an entity and 𝑛 binary relationships. Consider, for example, a ternary relationship, where Person 𝐴 sells Horse 𝐻 to Person 𝐵. Instead, one can reframe this data as a Sale entity 𝑆, a seller relationship from 𝑆 to 𝐴, a buyer relationship from 𝑆 to 𝐵, and an asset relationship from 𝑆 to 𝐻.

The term property graph was introduced by Rodriguez and Neubauer, though other terms were used to describe similar data models. Tsai and Fu’s attributed relational graph is a directed multigraph in which both nodes and edges have labels, and each label defines a set of numerical or logical attributes. Shao et al. used the term Heterogeneous graph for the same construct. Gallagher used the term data graph to refer to graphs in which vertices and/or edges may be typed and/or attributed. Singh et al. used the term M*3 (multi-modal, multi-relational, multifeatured) network to refer to graphs with multiple entity-types, multiple relationship-types, and multiple descriptive features for nodes and edges. Krause et al. used the term typed graph to refer to graphs with typed nodes, typed edges, and typed node properties.

Various extensions were proposed, including:

• Instead of a single label, each vertex has a (possibly empty) set of labels (vertex multi-labeled graph); entities are multi-typed
• Instead of a single label, each edge has a (possibly empty) set of labels (edge multi-labeled graph); relationships are multi-typed
• Directional relationship types naming: instead of a name for only one direction (e.g., owns), a unique name is defined for each direction (e.g., owns, owned by; parent of, offspring of)
• Property hypergraphs (hyperedges represent 𝑛-ary relationships)
• Schema-level and data-level metaproperties (properties of properties – e.g., units of measure, accuracy, reliability)
• EPGM – Extended Property Graph Model, in which logical graphs consist of subsets of a shared set of vertices and a shared set of edges. In addition, logical graphs have types and properties.
• Support of derivation (specialization) of entity-types, relationship-types, and property types

The Property Graph Schema

A schema is a model for describing the structure of information in a certain domain using a certain data model. A property graph schema defines the entity-types, the relationship-types, and the properties of thereof.

The property graph data model is schema-optional. Each property graph may be:

• Schema-free (schemaless, schema-independent). A schema-free property graph neither defines nor enforces entity-types or relationships-types; each vertex and edge, regardless of its label, may have properties with any name and of any data type.
• Schema-based (schema-strict, schema-driven, schema-full, schema-dependent). A schema-based property graph is a property graph conforming to a given schema.
• Schema-mixed (schema-hybrid), where a schema is defined, but additional elements (e.g., additional properties) may be used.

It is much easier to define patterns when the information is presented consistently. For example, to match patterns such as Any person who owns a white horse, one would first:

• Define entity-types Person and Horse
• Define a relationship-type owns that holds from entities of type Person to entities of type Horse
• For the Horse entity-type, define a color property with a nominal data type
• Ensure that all the information is structured accordingly

Though proposed property graph and property graph schema definitions have much in common (see Angles, Wu, Hartig and Hidders, and Angles et al.), to date, there is neither a de jure nor a de facto standard definition (and hence, no standard property graph schema definition language).

The following property graph schema model is assumed in this paper:

A property graph schema is defined by:

• A finite set of user-defined data types (on top of the built-in data types)
  • Categorical (nominal and ordinal) data types (e.g., gender: nominal {male, female})
  • Multivalued property data types (e.g., nicknames: set(string))
  • Composite data types (e.g., name {first: string, last: string}
  • Interval data types (e.g., span: interval(date))
• A finite set of entity-types. For each entity-type:
  • A unique name
  • A set of properties. For each property:
    • A unique name
    • A data type
    • For properties and subproperties with numeric data types, intervals of numeric data types, or multivalued numeric data types: an optional schema-level units metaproperty representing units of measure (e.g., Kg, cm, seconds)
• A finite set of relationship-types. For each relationship-type:
  • The relationship-type’s directionality: directional or bidirectional
  • A unique name
  • A set of pairs of entity-types for which the relationship-type is applicable (e.g., owns: {(Person, Horse), (Person, Dragon)}. When a pair is of the same type (e.g., (Dragon, Dragon)), loops can be allowed or disallowed
  • A set of properties - similar to entity-types’ properties

A predefined property-less entity-type Null serves two purposes:

• Realizing actions: an action-type can be realized as a relationship-type that is applicable between some entity-type and the Null entity-type. For example, a sleeps: {(Dragon, Null)} relationship-type realizes a sleeps action-type for the Dragon entity-type.
• Realizing relationships to unknown or unimportant entities: sometimes, a real entity is unknown or unimportant, but the existence of a relationship and the values of the relationship’s properties - are important. For example, we may know that a certain dragon was owned in a given timeframe, but we do not know or do not care who owned it. Still - we want to be able to store and query such information. owns: {(Person, Dragon), (Guild, Dragon), (Null, Dragon)} allows us to realize this.

Property graph schema definitions may vary in many aspects, including:

• Supported schema constraints (properties uniqueness and nullability, property value constraints, relationships cardinality constraints, disallow loops for certain relationship-types, etc.)
• Supported ways to declare user-defined data types
• Properties may be either:
  • Defined globally and assigned to one or more entity/relationship-types, or
  • Defined per entity/relationship-type: different entity/relationship-types may have a property with the same name but with a different data type

V1 can be utilized with most definitions with minimal changes.

Patterns and Pattern Languages

A pattern defines a set of topological and property value constraints on property graphs. Each property (sub)graph either matches the pattern or not. For some patterns, a given (sub)graph may match a pattern in more than one way.

When patterns are described in a natural language, they may be ambiguous, and the description may miss some nuances expressed in formal languages. Nevertheless, all the patterns below are described in English so that the reader may gain an intuitive understanding of their meaning.

Here are two examples:

• P1: Any person who owns at least five white horses (see Q101)

  P1 defines the set of (sub)graphs in which

  • There is a vertex 𝑝 with a label Person
  • There are 𝑛 ≥ 5 vertices ℎ₁..ℎₙ, each with a label Horse
  • Each of ℎ₁..ℎₙ has a color property, and its value is white
  • There are relationships from 𝑝 to ℎ₁..ℎₙ, each with a label owns

  Note that the pattern’s description ignores temporal aspects. Maybe a person has owned a horse, owns it, or will own it. Assuming that the owns relationship has a timeframe property, a more accurate description would be Any person who has ‘owns’ relationships with at least five white horses. Maybe we are looking for Any person who currently owns at least five white horses or for Any person who at some timepoint owned at least five white horses. If, for example, a horse’s color may change over time, or if a horse may turn into a unicorn, we might want to rephrase the pattern.

• P2: Any person whose date of birth is between January 1, 970 and January 1, 980, who owns a white Horse, who owns a dragon whose name starts with ‘M’ and over the last month froze at least three dragons belonging to members of the Masons Guild

  P2 defines the set of (sub)graphs in which

  • There is a vertex 𝑝 with a label Person
  • 𝑝 has a birthDate property of type date, and its value is between January 1, 970 and January 1, 980
  • There is at least one vertex ℎ with a label Horse
  • There is a relationship from 𝑝 to ℎ with a label owns
  • ℎ has a color property, and its value is white
  • There is at least one vertex 𝑑 with a label Dragon
  • There is a relationship from 𝑝 to 𝑑 with a label owns
  • 𝑑 has a name property with a value that starts with ‘M’
  • There are 𝑚 > 3 vertices, 𝑑₁..𝑑ₘ, each with a label Dragon
  • There are relationships from 𝑑 to any of 𝑑₁..𝑑ₘ, each with a label freezes
  • Each of these relationships has a tf property (stands for “timeframe”) with a since subproperty whose value is in the range [now - months(3) .. now]
  • There is a vertex 𝑔 with a label Guild
  • 𝑔 has a name property, and its value is Masons
  • There are 𝑛 ≥ 1 vertices 𝑞₁..𝑞ₙ, each with a label Person
  • There are relationships from each of 𝑞₁..𝑞ₙ to 𝑔, each with a label member of
  • There are relationships from each of 𝑞₁..𝑞ₙ to one or more of 𝑑₁..𝑑ₘ, each with a label owns. Each of 𝑑₁..𝑑ₘ is connected by at least one of these relationships

The terms entity and relationship denote both pattern elements and graph elements. When the context may be ambiguous, we use the terms pattern-entity and pattern-relationship to refer to pattern elements and the terms graph-entity and graph-relationship to refer to graph elements.

Given a property graph schema 𝑆, a property graph 𝐺 conforming to 𝑆, and a query pattern 𝑃 conforming to 𝑆, all expressed in language 𝐿 = (𝐿_𝑆, 𝐿_𝐺, 𝐿_𝑃, 𝐿_𝑅), pattern matching is the process of finding, transforming, merging, and annotating subgraphs of 𝐺 that match 𝑃. The syntaxes of sublanguages 𝐿_𝑆, 𝐿_𝐺, 𝐿_𝑃, and 𝐿_𝑅 define what and how symbols may be combined to form well-formed schemas, graphs, patterns, and query results, respectively. A semantics of 𝐿_P is a mapping (𝑆, 𝐺, 𝑃) → 𝑅: which subgraphs of 𝐺 match 𝑃 and how to transform, merge, and annotate them.

Any valid subgraph that matches the pattern is called an assignment. We use assignment to 𝑋 where 𝑋 is a pattern-entity, a pattern-relationship, or a set of thereof, to denote the graph-entity, the graph-relationship, or the set of thereof that matches 𝑋 as part of an assignment.

In the patterns given below, unless otherwise stated, each reported assignment should include the graph-entity assigned to each mentioned pattern-entity and the graph-relationship assigned to each mentioned pattern-relationship. Hence, any reported assignment to P1 should be composed of:

• A Person graph-entity
• Five or more Horse graph-entities, each of which has a color property, and its value is white
• The owns graph-relationships between the Person graph-entity to those Horse graph-entities

Consider the following alternative patterns:

• P1’: Any person who owns at least five white horses. Report only the person
• P1’’: Any person who owns at least five white horses. Report only the horses
• P1’’’: Any person who owns at least five white horses. Report the person and five of his horses

A query may be:

• A decision query: does at least one assignment exist?
• A counting query: how many assignments exist?
• A counting-decision query: are there at least 𝑘 assignments?
• A reporting query:
  • Report [all / up to 𝑘] subgraphs of 𝐺, each is an assignment
  • Report subgraphs of 𝐺, each is a union of assignments, e.g., the union of all assignments with identical assignments to all entities (and different assignments to relationships)
  • Report a single subgraph of 𝐺, composed of the union of all assignments. This is sometimes preferred since it avoids combinatorial explosion for many queries (e.g., if a person owns ten white horses, any subset of five of the person’s horses compose an assignment to P1’'’). However, for some patterns, individual assignments cannot be deduced from their union.

Implementations may support one or more of the above.

V1 introduces the concept of calculated properties - non-inherent properties of graph-entities, graph-relationships, and subgraphs, defined as part of a pattern. Each calculated property’s evaluation result can be part of the reported query results, extending V1 capabilities beyond ‘simple’ pattern matching. For example, The average number of horse ownerships per person - a calculated property of the set of all graph-entities of type Person can be defined as part of a pattern. See Q356).

Pattern languages differ in many aspects, including:

• Genericity - general-purpose (e.g., schema-driven) vs. domain-specific
• Pattern representation - textual vs. visual (graphical, diagrammatic)
• Receptivity and Productivity (i.e., readability and writability) - how intuitive and straightforward is it to understand existing patterns and construct new ones
• Conciseness - the fewness of symbols and symbol types required for expressing patterns
• Aesthetics - the quality of patterns being visually appealing
• Declarative / Imperative - Declarative languages describe patterns but do not specify how to match them. Imperative languages describe patterns in terms of the steps required to match them on a given computational machine model (e.g., the Gremlin Traversal Machine). Languages may provide both declarative and imperative constructs.
• Expressive power - the breadth of patterns that can be expressed. Unless a pattern language (declarative or imperative) is Turing-complete, there would always be computable patterns that cannot be expressed.

There are always tradeoffs, especially between receptivity and productivity and expressive power. Quoting Perlis’ 54th and 55th epigrams of programming: “Beware of the Turing tar-pit in which everything is possible but nothing of interest is easy.” and “A LISP programmer knows the value of everything, but the cost of nothing.” Perlis’ 93rd and 26th epigrams are also worth quoting here: “When someone says, ‘I want a programming language in which I need only say what I wish done,’ give him a lollipop.” and “There will always be things we wish to say in our programs that in all known languages can only be said poorly.” Though these epigrams refer to programming languages, they are equally valid for property graph query languages.

A Song of Ice and Fire

The following scenario, loosely based on George R. R. Martin’s A Song of Ice and Fire will serve us to demonstrate the language’s expressive power.

The subjects of Sarnor, Omber, and the other kingdoms of the known world love their horses. There is one thing they adore even more - that is their dragons. They own dragons of ice and fire. Like all well-behaved dragons, their dragons love to play. Dragons always play in couples. When playing, dragons often get furious, fire at each other (fire breath), and freeze one another (cold breath). Dragons usually freeze one another for periods of several minutes. However, on occasion, when they are furious, they can freeze one another for periods of several hours. The subjects enjoy watching their dragons play. Fascinated by these magnificent creatures, they have composed myriads of scrolls detailing each fire breath and cold breath over the last thousand years. The kings of Sarnor and Omber regularly pose queries about their history. More than often, it takes the royal historians and royal analysts several days to come up with answers, during which the kings tend to get pretty impatient. Lately, the high king of Sarnor posed a very complex query. After waiting for results for more than two moons, he ordered the chief analyst to be executed. He then summoned his chief mechanics and ordered them to develop an apparatus that he could use to pose queries and get results quickly.

The engineers started by collecting all queries posed by their master over the last few years. Then they constructed a property graph schema over which these queries can be expressed.

The schema was composed of the following entity-types (and their properties):

• Person: name {first: string, last: string}, gender: nominal {male, female}, birthDate: date, deathDate: date, height: int [cm]
• Dragon: name: string, color: nominal {black, white, …}
• Horse: name: string, color: nominal {black, white, …}, weight: int [Kg]
• Guild: name: string
• Kingdom: name: string

the following directional relationship-types (and their properties):

• owns: {(Person, Horse), (Person, Dragon), (Guild, Horse), (Guild, Dragon)} - df: dateframe

  When the person is still the owner and the ownership has no defined termination date (the value in inapplicable), df.till is 31/12/9999.

• fires at: {(Dragon, Dragon)} - time: datetime; no loops allowed

• freezes: {(Dragon, Dragon)} - tf: datetimeframe; no loops allowed

  tf is set only after the freeze has ended. tf.since and tf.till are non-nullable.

• offspring of: {(Person, Person)}; no loops allowed

• member of: {(Person, Guild)} - df: dateframe

  When the person is still a member and the membership has no defined termination date (the value in inapplicable), df.till is 31/12/9999.

• subject of: {(Person, Kingdom)}

and of the following bidirectional relationship-type (and its properties):

• friend of: {(Person, Person)} - since: date; no loops allowed

Person’s name is a composite property. The date, datetime, dateframe, and datetimeframe data types are defined in Data Types, Operators, and Functions.

The engineers then represented the whole known history using a property graph conforming to this schema.

V1 Basics

The following sections describe the syntax and the semantics of the V1 language. We start with the basics, adding more language elements as we go along.

Note: V1 has two equivalent syntaxes for expressing patterns: A visual syntax - described below, and a textual syntax (JSON-based) - summarized here. There is a bijective mapping between patterns expressed in these two syntaxes. Sample textual patterns are available here. A V1 schema for A Song of Ice and Fire is available here.

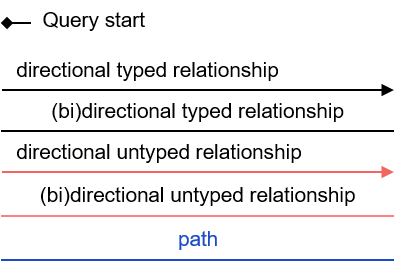
Patterns are generally read from left to right. Each pattern starts with a small black diamond, denoting the pattern start. The most straightforward patterns are structured as a sequence of rectangles, where consecutive rectangles are connected with an arrow or a line.

Yellow, blue, and red rectangles represent concrete, typed and untyped entities, respectively. The terms concrete entity, typed entity, and untyped entity refer to pattern entities only (and not to graph entities).

A yellow rectangle represents a concrete entity: a specific person, a specific horse, etc. A concrete entity has a single assignment - a specific graph-entity. The text inside the rectangle denotes the entity-type and the value of a visualization expression defined for this entity-type. For example, the visualization-expression for the Person entity-type may be: name.first ∥ ‘ ‘ ∥ name.last and its value, for a specific graph-entity, would be ‘Brandon Stark’.

A blue rectangle represents a typed entity. The text inside the rectangle denotes an entity-type. Only graph-entities of this type may be assigned to the pattern-entity.

A red rectangle represents an untyped entity. Graph-entities of different types may be assigned to an untyped entity. An optional text inside the rectangle denotes an entity-type constraint (See Untyped Entities).

Two consecutive rectangles can be connected with:

• A horizontal black arrow, representing a directional typed relationship,
• A horizontal black line, representing either a bidirectional typed relationship or a directional typed relationship for which either direction is acceptable,
• A horizontal red arrow, representing an untyped directional relationship (see Untyped Relationships),
• A horizontal red line, representing either an untyped bidirectional relationship or an untyped directional relationship where either direction is acceptable, or
• A horizontal blue line, representing a pattern-path (see Paths)

The terms typed relationship and untyped relationship refer only to pattern relationships. The term path may refer to both graph-path and pattern-path.

Each black arrow/line has a label on top. The label denotes a relationship-type. For arrows - the label is aligned to the arrow’s origin. For lines - the label is centered. Only graph-relationships of this type can match the pattern-relationship.

A pattern matching engine would look in the property graph for assignments for every blue rectangle, red rectangle, black arrow, and black line. Graph entities are assigned to pattern entities. Graph relationships are assigned to pattern relationships. An assignment to the pattern is a set of graph-entities and graph-relationships that matches the whole pattern.

The relationship-type between any two entities must be valid with respect to the schema.

Q1: Any dragon owned by Brandon Stark (two versions)

Q2: Any dragon C that at least once had been frozen by a dragon owned by Brandon Stark

Q184: Any dragon C that at least once froze a dragon owned by Brandon Stark or was frozen by a dragon owned by Brandon Stark

Both directions of the freezes relationship are acceptable. Therefore - a line (instead of an arrow) is used in the pattern.

Expressions and Expression Constraints

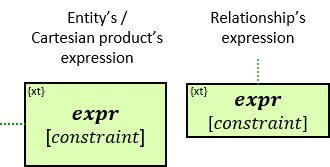
A green rectangle represents an expression. The rectangle contains:

• An expression-tag (‘{xt}’) (see Expression-Tags)
• An expression (‘expr’)
• An optional constraint on the result of the evaluation of the expression, composed of:
  • A constraint operator
  • A constraint expression (except when the constraint operator is is null or not null)
• When units of measure are defined for the expression (based on the units of measures of the properties and the operators that compose the expression) - they are depicted as well (see Q117, Q304, Q265, Q95).

expr is an entity’s expression, a relationship’s expression, or a Cartesian product’s expression, or a global expression.

• An entity’s expression

  The expression is composed of or depends on at least one property (inherent or calculated) of the connected entity and no properties of other entities/relationships.

  The green rectangle is connected to a pattern-entity (concrete, typed, or untyped) on its left.

  An expression-tag of an entity’s expression is a property of each unique assignment to the pattern-entity.

• A relationship’s expression

  The expression is composed of or depends on at least one property (inherent or calculated) of the connected relationship and no properties of other entities/relationships.

  The green rectangle is connected to a pattern-relationship on its top.

  An expression-tag of a relationship’s expression is a property of each unique assignment to the pattern-relationship (Note that it is not a property of an assignment to the Cartesian product of the two related entities).

• A Cartesian product’s expression

  The expression is composed of or depends on properties (inherent or calculated) of at least two entities (see {3} in Q207, {2}, {3} and {4} in Q340), at least two relationships (see {2} in Q267v2), or at least one entity and one relationship (see {1} in Q115v2, {2} and {4} in G3).

  The green rectangle is connected to one of the entities/relationships or located at the same level as the leftmost entities (when there is no single leftmost entity) (see Q207).

  An expression-tag of a Cartesian product’s expression is a property of each unique assignment to the Cartesian product.

  See also extended Cartesian product’s expression in Extended Aggregators.

• A global expression

  The expression is composed of and depends on no entity’s expression, relationship’s expression, nor Cartesian product’s expression.

  The green rectangle is located at the same level as the leftmost entities (see Q375).

  A global expression is a global property.

Any expression-tag of an expression that is not a property name, a subproperty name, or a constant is called a calculated property.

An expression is

• A literal (string, integer, or float),

  Note: date, datetime, and duration literals are represented using the functions date(string), datetime(string) and duration(string), respectively. In visual syntax, these function names are omitted, and expressions are formatted according to the regional settings (see Q8),

• <_inherent property="" name_=""> (of a connected entity/relationship) (valid for a Cartesian product's expression only if it is connected to an entity/relationship),
• <_inherent property="" name_="">.<_subproperty name_="">[.<_subproperty name_=""> ...] (of a connected entity/relationship) (valid for a Cartesian product's expression only if it is connected to an entity/relationship),
• An expression-tag or an aggregation-tag (e.g., ‘{1}’),
• op expr, where op is a unary operator (e.g., ‘- {1}’),
• expr op expr, where op is a binary operator (e.g., ‘3 + {1}’),
• (expr),
• ‘𝑓’ where 𝑓 is a parameterless function (e.g., ‘now’. See G11),
• ‘𝑓(e1, e2, …)’ where 𝑓 is a function with at least one parameter and e1, e2, … are expressions (see Q353),
• ‘e1.𝑓’ - equivalent to 𝑓(e1), where 𝑓 is a function with one parameter and e1 is an expression,
• ‘e1.𝑓(e2, e3, …)’ - equivalent to 𝑓(e1, e2, e3, …), where 𝑓 is a function with more than one parameter and e1, e2, e3, … are expressions,
• An interval expression (see Q327),
• A set expression (see Q318),
• A bag expression (see Q315), or
• A list expression

An interval can be explicitly constructed using the following syntaxes:

• (expr1 .. expr2) - an open interval
• (expr1 .. expr2] - a half-open interval
• [expr1 .. expr2) - a half-open interval

• [expr1 .. expr2] - a closed interval

  Both expr1 and expr2 are of the same ordinal data type.

  if expr1 > expr2 - the interval is an empty interval.

  if expr1 = expr2 - (expr1 .. expr2), (expr1 .. expr2], [expr1 .. expr2) are empty intervals.

  If expr1, expr2, or both are evaluated to null - the interval is evaluated to null.

A set is an unordered collection of zero or more non-null values (called elements) of the same data type in which each element may occur only once.

A set can be explicitly constructed using the following syntax:

• {expr, expr, …} - zero or more expressions of the same data type. null values are ignored. Duplicate values are merged.

  A comma after the last element is optional, except for a single-element set where it is mandatory.

A bag (multiset) is an unordered collection of zero or more non-null values (called elements) of the same data type in which elements may occur more than once.

A bag can be explicitly constructed using the following syntax:

• [expr, expr, …] - zero or more expressions of the same data type. null values are ignored.

  A comma after the last element is optional.

  Bag elements are unordered, and duplicates are allowed. A bag may not contain null values.

A list is an ordered collection of values (called elements) of the same data type in which elements may occur more than once.

A list can be explicitly constructed using the following syntax:

• (expr, expr, …) - zero or more expressions of the same data type.

  A comma after the last element is optional, except for a single-element list where it is mandatory.

Expressions must match the data types defined for each operator and function.

A constraint filters assignments; an assignment is valid only if the result of the expression’s evaluation satisfies the constraint.

A constraint cannot be defined for a concrete entity’s expression.

For untyped entities, expressions can be composed only of properties common to all valid entity-types. Valid entity-types for an untyped entity are defined implicitly (according to the types of the pattern-entities and pattern-relationships which are connected to the untyped entity) or explicitly (using entity-type constraints - see later) (see Q291).

A subproperty of a composite property is denoted as <_property name_="">.<_subproperty name_=""> (e.g., _name.first_, _tf.since_).

Q3: Any person whose first name is Brandon who owns a dragon (version 1)

{1} is a property of each unique assignment to B.

Q190: Any person who became a dragon owner at 1011 or later (two versions)

{1} is a property of each unique assignment to the owns relationship.

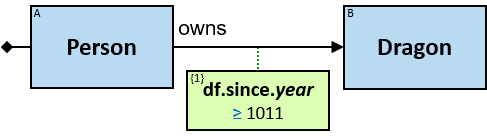
year is a function (see next section).

All V1 constraint operators, except is null and not null, are first evaluated using Kleene’s three-valued logic (3VL) to true, false, or unknown, and then mapped to a two-valued logic: the constraint is either satisfied or not satisfied.

Each constraint operator, except is null and not null, can be either blue or red.

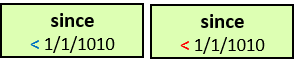
• A blue constraint operator: the constraint is satisfied if and only if it is evaluated to true
• A red constraint operator: the constraint is satisfied if and only if it is evaluated to true or to unknown

The following constraint operators can be only blue:

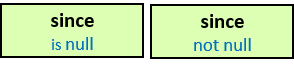
• A is null constraint is satisfied if and only if the expression is evaluated to null
• A not null constraint is satisfied if and only if the expression is not evaluated to null

Data Types, Operators, and Functions

All V1’s operators and functions must be well-defined when one or more of the operands or parameters are null or evaluated to null. Null-valued [sub]properties are interpreted as applicable missing or no information (e.g., 1 + null = null; max(5, null) = null).

Since V1 is schema-based, there is no need to define the behavior of each operator for any combination of operand types (and similarly, for each function for any combination of parameter types). When types do not match the definition (e.g., 5 > ‘abc’, round(‘abc’)) – the query is invalid. Type mismatch should be detected during query analysis. In addition, interactive pattern-building tools should disallow the construction of such queries.

One design goal of V1 is to make it applicable to many property graph database management systems. Implementations may support different data types, operators, and functions than those presented here.

To present V1, we use the following data types, operators, and functions:

Built-in basic data types:

Type	Notes
int	Integer
float	Floating-point
date	Date. For simplicity, we will not consider time zones here.
datetime	Date and time. For simplicity, we will not consider time zones here.
duration	Can be negative
string	Unicode string

Built-in composite data types:

Type	Notes
dateframe	{since: date, till: date}
datetimeframe	{since: datetime, till: datetime}

Literals:

Type	Examples
integer	12, -3
float	3., 3.12, -1.78e-6, NaN, -INF, +INF
string	””, “abc”, ‘abc’

We will use St, Bt, and Lt, to denote a set, a bag, and a list of elements of type 𝑡, respectfully, and It to denote an interval of ordinal type 𝑡.

Operators:

Operator (op)	Operands and result type (result may be null as well)
+, - (unary)	op int → int op float → float If the operand is NaN – the result is NaN. Otherwise, If it is null – the result is null
+, - (binary)	int op int → int float op float → float duration op duration → duration duration + date → date date op duration → date duration + datetime → datetime datetime op duration → datetime If one or both operands are NaN – the result is NaN. Otherwise, if one or both operands are null – the result is null
*	int * int → int float * float → float float * duration → duration duration * float → duration If one or both operands are null - the result is null
/	int / int → int (truncated towards zero) float / float → float duration / float → duration If one or both operands are null - the result is null
% (modulo)	int % int → int (remainder has the same sign as the dividend) If one or both operands are null - the result is null
∪, ∩, -, △ (union, intersection, difference, symmetric difference)	St op St → St (𝑡 is any type) Bt op Bt → Bt (𝑡 is any type) (see Q377) If one or both operands are null - the result is null
∥ (concatenation)	string ∥ string → string. 𝑠 ∥ null = null ∥ 𝑠 = null Lt ∥ Lt → Lt (𝑡 is any type). null ∥ 𝐿 = 𝐿 ∥ null = null 𝑡 ∥ Lt → Lt (𝑡 is any type). null ∥ 𝐿 = (null, …). 𝐿. 𝑡 ∥ null = null Lt ∥ 𝑡 → Lt (𝑡 is any type). 𝐿 ∥ null = (…, null). null ∥ 𝑡 = null

Constraint Operators:

Operator (op)	Operands type (result is false / true / unknown)
is null, not null (unary)	any_type op An empty set / bag / list is not a null value.
=, ≠	both operands of the same type (any type) unknown if at least one operand is null Exceptions for float: (NaN = null) = false; (NaN ≠ null) = true
<, >, ≤, ≥	both operands of the same ordinal type: int / float / date / datetime / duration / string / other ordinal unknown if at least one operand is null. Exceptions for string: (“” ≤ null) = (null ≥ “”) = true (“” > null) = (null < “”) = false (“” > null) = (null < “”) = false Exceptions for float: (null ≤ NaN) = (null ≥ NaN) = (null < NaN) = (null > NaN) = false (NaN ≤ null) = (NaN ≥ null) = (NaN < null) = (NaN > null) = false Exceptions for bounded types with no NaN value: (lb ≤ null) = (null ≥ lb) = (ub ≥ null) = (null ≤ ub) = true (ub < null) = (null > ub) = (lb > null) = (null < lb) = false where lb is the lower bound (e.g., INT_MIN for integer) and hb is the upper bound (e.g., INT_MAX for integer)
∈, ∉ ([not] in)	left operand: any type 𝑡. right operand: St / Bt / Lt unknown if at least one operand is null. Exceptions: (null ∈ {}/[]/()) = false; (null ∉ {}/[]/()) = true left operand: any ordinal type 𝑡. right operand : It unknown if at least one operand is null. Exceptions: (null ∈ empty interval) = false; (null ∉ empty interval) = true 𝑡 is int: (null ∈ [INT_MIN, INT_MAX]) = true; (null ∉ [INT_MIN, INT_MAX]) = false
∋, ∌ ([not] contains)	right operand: any type 𝑡. left operand: St / Bt / Lt unknown if at least one operand is null. Exceptions: ({}/[]/() ∋ null) = false; ({}/[]/() ∌ null) = true right operand: any ordinal type 𝑡. left operand : It unknown if at least one operand is null. Exceptions: (empty interval ∋ null) = false; (empty interval ∌ null) = true 𝑡 is int: ([INT_MIN, INT_MAX] ∋ null) = true; ([INT_MIN, INT_MAX] ∌ null) = false
⊆, ⊈ ([not] sub of) ⊂, ⊄ ([not] proper sub of)	both operands: string unknown if at least one operand is null. Exceptions: (null ⊂ “”) = false; (null ⊄ “”) = true (“” ⊆ null) = true; (“” ⊈ null) = false both operands of the same type: St / Bt / Lt (t is any type) unknown if at least one operand is null. Exceptions: (null ⊂ {}/[]/()) = false; (null ⊄ {}/[]/()) = true ({}/[]/() ⊆ null) = true; ({}/[]/() ⊈ null) = false 𝑡 is ordinal, and both operands of the same type: It unknown if at least one operand is null. Exceptions: (null ⊂ empty interval) = false; (null ⊄ empty interval) = true (empty interval ⊆ null) = true; (empty interval ⊈ null) = false 𝑡 is int: (null ⊂ [INT_MIN, INT_MAX]) = true; (null ⊄ [INT_MIN, INT_MAX]) = false
⊇, ⊉ ([not] super of) ⊃, ⊅ ([not] proper super of)	both operands: string unknown if at least one operand is null. Exceptions: (null ⊇ “”) = true; (null ⊉ “”) = false (“” ⊃ null) = false; (“” ⊅ null) = true both operands of the same type: St / Bt / Lt (t is any type) unknown if at least one operand is null. Exceptions: (null ⊇ {}/[]/()) = true; (null ⊉ {}/[]/()) = false ({}/[]/() ⊃ null) = false; ({}/[]/() ⊅ null) = true 𝑡 is ordinal, and both operands of the same type: It unknown if at least one operand is null. Exceptions: (null ⊇ empty interval) = true; (null ⊉ empty interval) = false (empty interval ⊃ null) = false; (empty interval ⊅ null) = true 𝑡 is int: ([INT_MIN, INT_MAX] ⊃ null) = true; ([INT_MIN, INT_MAX] ⊅ null) = false
⊳, ⋫ ([not] starts with)	both operands: string unknown if at least one operand is null. Exceptions: (null ⊳ “”) = true; (null ⋫ “”) = false left operand: Lt. right operand: 𝑡 (𝑡 is any type) unknown if at least one operand is null. Exceptions: (() ⊳ null) = false; (() ⋫ null) = true left operand: Lt. right operand: Lt (𝑡 is any type) unknown if at least one operand is null. Exceptions: (null ⊳ ()) = true; (null ⋫ ()) = false
⊲, ⋪ ([not] ends with)	both operands: string unknown if at least one operand is null. Exceptions: (null ⊲ “”) = true; (null ⋪ “”) = false left operand: Lt. right operand: 𝑡 (𝑡 is any type) unknown if at least one operand is null. Exceptions: (() ⊲ null) = false; (() ⋪ null) = true left operand: Lt. right operand: Lt (𝑡 is any type) unknown if at least one operand is null. exceptions: (null ⊲ ()) = true; (null ⋪ ()) = false
≍, ≭ ([not] match)	both operands: string (right operand is a regex string) unknown if at least one operand is null. Exceptions: (null ≍ “”) = true; (null ≭ “”) = false

Implicit Type Coercion

From type (t1)	To type (t2)	Examples
int	float	5 + 3. → 8.
date	datetime	date(“2018-04-05”) = datetime(“2018-04-05T00:00:00”) → true
dateframe	datetimeframe	dateframe(“2018-04-05”, “2018-04-08”) = datetimeframe(“2018-04-05T00:00:00”, “2018-04-08T23:59:59.999999999”)
dateframe	interval(date)	df.duration, where df is a dateframe property
datetimeframe	interval(datetime)	tf.duration, where tf is a datetimeframe property
interval(date)	dateframe	(date(“2018-04-05”) .. date(“2018-05-05”)).since → date(“2018-04-05”)
interval(datetime)	datetimefrmae	(date(“2018-04-05”) .. datetime(“2018-05-05T00:00”)).since → datetime(“2018-04-05T00:00”)

Also, based on any of these coercion rules:

From type	To type	Examples
{} (empty set)	set(t2) of any type t2	{} ∪ {5} → {5}
[] (empty bag)	bag(t2) of any type t2	[] ∪ [5] → [5] (see Q349)
() (empty list)	list(t2) of any type t2	() ∥ (5,) → (5,)
set(t1)	set(t2)	{3, 5, 8} ∪ {3., 8.) → {3., 5., 8.}
bag(t1)	bag(t2)	[3, 5, 8] ∪ [3., 8.] → [3., 3., 5., 8., 8.]
list(t1)	list(t2)	(3, 5, 8) ∥ (3., 8.) → (3., 5., 8., 3., 8.)
interval(t1)	interval(t2)	(3 .. 8) = (3. .. 8.) → true (3 .. 8) ⊃ (3. .. 5.) → true
{t1, t2, …}	set(t2) *	{3, 5.) → {3., 5.)
[t1, t2, …]	bag(t2) *	[3, 5.] → [3., 5.]
(t1, t2, …)	list(t2) *	(3, 5.) → (3., 5.)
t1 .. t2	interval(t2) *	[3 .. 5.) → [3. .. 5.)

* where there is implicit type coercion from t1 to t2

Functions

Functions over float expressions:

Function	Notes
trunc(float) → int	truncates toward zero
round(float) → int	rounds to the nearest integer (see G13)
mRound(float, int) → int	rounds to the nearest multiple of a given integer (see G9, G10)
seconds(float) → duration	(e.g., seconds(6) is a duration of 6 seconds)
minutes(float) → duration	See G10
hours(float) → duration
days(float) → duration	See Q216, Q289
weeks(float) → duration	One week = 7 days
months(float) → duration	One month = 30.4367 days (see Q110)
years(float) → duration	One year = 365.24 days (see Q317)

Functions over string expressions:

Function	Notes
length(string) → int	See Q255
toLower(string) → string	See Q308
date(string) → date	String format: YYYY-MM-DD (e.g., “2018-04-23”) In visual syntax the, function name is omitted, and the string is formatted according to the regional settings.
datetime(string) → datetime	String format: YYYY-MM-DDTHH:MM[:SS[.sss]] (e.g., “2018-04-23T12:34:00”) In visual syntax, the function name is omitted, and the string is formatted according to the regional settings.
duration(string) → duration	String format adapted from Cypher: P[nY][nM][nW][nD][T[nH][nM][nS]] (e.g., “P1Y2M10DT12H45M30.25S”) Y: years, M: months, W: weeks, D: days, H: hours, M: minutes, S: seconds In visual syntax, the function name is omitted, and the string is formatted.

Functions over datetime expressions:

Function	Notes
date(datetime) → date	See Q158
year(datetime) → int	See Q185
month(datetime) → int	The month of the year (1-12)
day(datetime) → int	The day of the month (1-31)
hour(datetime) → int	0-23 (see G4)
minute(datetime) → int	0-59
sec(datetime) → int	0-59
yearsSinceEpoch(datetime) → float
monthsSinceEpoch(datetime) → float
weeksSinceEpoch(datetime) → float
daysSinceEpoch(datetime) → float
hoursSinceEpoch(datetime) → float
minsSinceEpoch(datetime) → float
span(datetime, datetime) → duration	Positive difference (see Q374)

Functions over date expressions:

Function	Notes
year(date) → int
month(date) → int	The month of the year (1-12)
day(date) → int	The day of the month (1-31)
yearsSinceEpoch(date) → float
monthsSinceEpoch(date) → float
weeksSinceEpoch(date) → float
daysSinceEpoch(date) → float

Functions over dateframe expressions:

Function	Notes
duration(dateframe) → duration
overlap(dateframe, dateframe) → duration	Always non-negative (see Q267v2)

Functions over datetimeframe expressions:

Function	Notes
duration(datetimeframe) → duration	See Q110
overlap(datetimeframe, datetimeframe) → duration	Always non-negative

Functions over duration expressions:

Function	Notes
years(duration) → float	One year = 365.24 days
months(duration) → float	One month = 30.4367 days
weeks(duration) → float	One week = 7 days
days(duration) → float	See Q328
hours(duration) → float
minutes(duration) → float
seconds(duration) → float

Functions over set expressions:

Function	Notes
count(St) → int	number of elements
bag(St) → Bt	set to bag
list(St) → Lt	set to list
el(St) ⇉ 𝑡	(see Multivalued Functions and Expressions)
subset(St) ⇉ St	(see Multivalued Functions and Expressions)
min(St) → 𝑡 max(St) → 𝑡	𝑡 is an ordinal type null when St is null or when it is empty
avg(St) → 𝑡 or float	𝑡 is an ordinal type if 𝑡 is int - the result is float null when St is null or when it is empty
sum(St) → 𝑡	𝑡 is int / float / duration (not date / time / datetime) null when St is null; zero when it is empty
min(St, n: int) → St max(St, n: int) → St	Set of (up to) max(0, 𝑛) smallest/largest values 𝑡 is an ordinal type null when St is null, {} when it is empty
overlap(Sdateframe) → duration overlap(Sdatetimeframe) → duration	The duration of the overlap between all members of 𝑆 Always non-negative (see Q371)
union(SSt) → St union(SBt) → Bt	The union of all members of a set of sets/bags (𝑡 is any type)
intersection(SSt) → St intersection(SBt) → Bt	The intersection of all members of a set of sets/bags (𝑡 is any type)

Functions over bag expressions:

Function	Notes
count(Bt) → int	number of elements
distinct(Bt) → int	number of distinct elements
multiplicity(Bt, 𝑡) → int	number of times 𝑡 occurs in Bt
set(Bt) → St	bag to set
list(Bt) → Lt	bag to list
el(Bt) ⇉ 𝑡	(see Multivalued Functions and Expressions)
subbag(Bt) ⇉ Bt	(see Multivalued Functions and Expressions)
min(Bt) → 𝑡 max(Bt) → 𝑡	𝑡 is an ordinal type null when Bt is null or when it is empty
avg(Bt) → 𝑡 or float	𝑡 is an ordinal type if 𝑡 is int - the result is float null when Bt is null or when it is empty
sum(Bt) → 𝑡	𝑡 is int / float / duration (not date / time / datetime) null when Bt is null; zero when it is empty
min(Bt, n: int) → Bt max(Bt, n: int) → Bt	Bag of (up to) max(0, 𝑛) smallest/largest values (see Q377) 𝑡 is an ordinal type null when Bt is null, [] when it is empty
overlap(Bdateframe) → duration overlap(Bdatetimeframe) → duration	The duration of the overlap between all members of 𝐵 Always non-negative
union(BSt) → St union(BBt) → Bt	The union of all members of a bag of sets/bags (𝑡 is any type)
intersection(BSt) → St intersection(BBt) → Bt	The intersection of all members of a bag of sets/bags (𝑡 is any type)

Functions over list expressions (𝑡):

Function	Notes
count(Lt) → int	number of elements
distinct(Lt) → int	number of distinct non-null elements
multiplicity(Lt, 𝑡) → int	number of times 𝑡 occurs in Lt
at(Lt, n: int) → t	𝑛’th element (1-based) null if 𝑛 is out of range
set(Lt) → St	list to set
bag(Lt) → Bt	list to bag
min(Lt) → 𝑡 max(Lt) → 𝑡	𝑡 is an ordinal type null values are ignored null when Lt is null or when it contains no non-null elements
avg(Lt) → 𝑡 or float	𝑡 is an ordinal type if 𝑡 is int - the result is float null values are ignored null when Lt is null or when it contains no non-null elements
sum(Lt) → 𝑡	𝑡 is int / float / duration (not date / time / datetime) null values are ignored zero when Lt is null or when it contains no non-null elements
min(Lt, n: int) → Lt max(Lt, n: int) → Lt	List of (up to) max(0, 𝑛) smallest/largest values 𝑡 is an ordinal type null values are ignored null when Lt is null, () when it contains no non-null elements
sort(Lt) → Lt	Sorted list 𝑡 is an ordinal type
invsort(Lt) → Lt	Inverse-sorted list 𝑡 is an ordinal type

Functions over interval expressions:

Function	Notes
lb(It) → 𝑡	Lower bound null when It is null
up(It) → 𝑡	Upper bound null when It is null
set(It) → St	Interval to set 𝑡 is discrete (int, datetime, or another ordinal type) null when It is null
bag(It) → Bt	Interval to bag 𝑡 is discrete (int, datetime, or another ordinal type) null when It is null
list(It) → Lt	Interval to list 𝑡 is discrete (int, datetime, or another ordinal type) null when It is null

Other functions:

Function	Notes
now → datetime	See Q8v2, G11
today → date	See Q328
date(year, month, day) → date	Construct date using three integers (see Q353) null when at least one value is null
min(𝑡, 𝑡, …) → 𝑡 max(𝑡, 𝑡, …) → 𝑡	One or more values of the same ordinal type null when at least one value is null min({𝑡, 𝑡, …})and max({𝑡, 𝑡, …}) ignore null values (see Q317)

Implementations may support opaque data types - data types for which the internal data representation is not exposed. For each opaque data type - a set of functions and operators may be defined (see location data type in Application: Spatiotemporality).

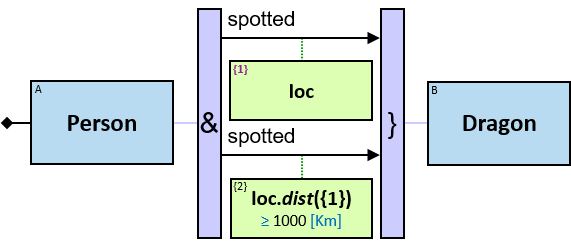
Quantifiers

A vertical purple rectangle represents a vertical quantifier. The text inside the rectangle denotes the quantifier type.

Vertical quantifiers (or simply ‘quantifiers’) add much expressive power, including more complex topological constraints, more than one entity’s expression constraint, and alternative subpatterns.

Q3: Any person whose first name is Brandon who owns a dragon (version 2)

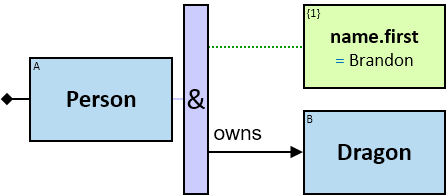
Q219: Any person who owns a white horse weighing more than 200 Kg

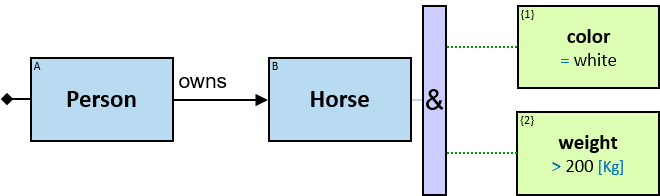
Q304: Any person who owns a white horse and who owns a horse weighing more than 200 Kg

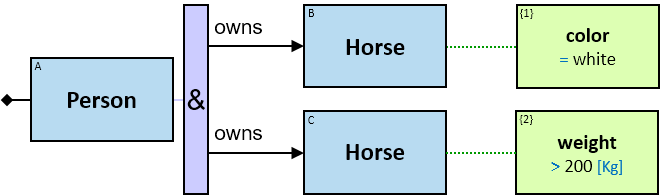
The same graph-entity may match more than one pattern-entity. For example, Either the same horse or different horses may be assigned to B and C (this can be avoided: see identicality, nonidenticality, and order constraints later on). Similarly, the same graph-relationship may match more than one pattern-relationship.

A vertical quantifier has one connection on its left side and zero or more branches on its right side. On its left side is an entity, a quantifier, or the pattern’s start. Except at the pattern’s start, a quantifier may be wrapped with an ‘O’ (see Q147, Q360v2).

When a quantifier (or the rightmost quantifier in a sequence of quantifiers) is directly right of the pattern start, each branch may start with:

• An entity (see Q108),
• A Cartesian product’s expression (see Q207)
• A global expression (see Q375), or
• A quantifier (see Q332v2)

When a quantifier (or the rightmost quantifier in a sequence of quantifiers) is directly right of an entity, each branch may start with:

• A relationship/path
  • optionally, with a relationship/path-negator (see Q358, Q359)
  • optionally, with a negator or with an ‘O’ (see Q358, Q359)
  • optionally, with relationship’s expressions (see Q339)
  • optionally, with aggregators (see Q125),
• An entity’s expression (see Q3v2),
• A Cartesian product’s expression (see Q340), or
• A quantifier (see Q8)

The following branches do not affect the quantifier’s evaluation:

• Any branch composed of an entity’s expression with no constraint (see Q109)
• Any branch that starts with an ‘O’ (see Q148)

Each such branch is marked with a white triangle.

All other branches affect the quantifier’s evaluation. Let 𝑏 denote the number of such branches.

We will name the left side of the quantifier the left component, and anything that follows a branch, up to the branch’s end, a right component.

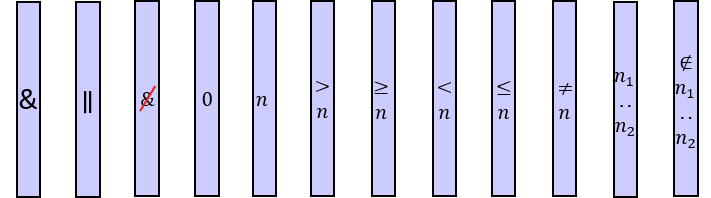
12 quantifier types are defined:

• All (denoted ‘&’)

  If 𝑏 is zero, an assignment matches the pattern if and only if it matches the left component. Otherwise - An assignment matches the pattern if and only if it matches the whole pattern.

• Some (denoted ‘|’)

  If 𝑏 is zero, no assignment matches the pattern. Otherwise - An assignment matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • 𝑄 has 𝑖 right components identical to 𝑃’s, 1 ≤ i ≤ b, and no other right components
  • The quantifier is replaced with an All quantifier

• Not all (but more than 0) (denoted by an ‘&’ with stroke)

  If 𝑏 is zero, no assignment matches the pattern. Otherwise - An assignment 𝐴 matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • 𝑄 has 𝑖 right components identical to 𝑃’s, 1 ≤ i < b, and no other right components
  • The quantifier is replaced with an All quantifier

  and there is no assignment 𝐵 with a similar left component as 𝐴’s that matches pattern 𝑅 where

  • 𝑅’s left component and all its right components are identical to 𝑃’s
  • The quantifier is replaced with an All quantifier

• None (denoted ‘0’)

  If 𝑏 is zero, an assignment matches the pattern if and only if it matches the left component. Otherwise - An assignment 𝐴 matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • The quantifier and the right components are removed

  and there is no assignment 𝐵 with a similar left component as 𝐴’s that matches pattern 𝑅 where

  • 𝑅’s left component is identical to 𝑃’s
  • 𝑅 has 𝑖 right components identical to 𝑃’s, 1 ≤ i ≤ b, and no other right components
  • The quantifier is replaced with an All quantifier

  The None quantifier may not start a pattern.

• = 𝑛; 𝑏 ≥ 1, 𝑛 ∈ [1,𝑏]

  An assignment 𝐴 matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • 𝑄 has 𝑛 right components identical to 𝑃’s, and no other right components
  • The quantifier is replaced with an All quantifier

  and, if n ≠ b, there is no assignment 𝐵 with a similar left component as 𝐴’s that matches pattern 𝑅 where

  • 𝑅’s left component is identical to 𝑃’s
  • 𝑅 has 𝑖 right components identical to 𝑃’s, 𝑖 > 𝑛, and no other right components
  • The quantifier is replaced with an All quantifier

• > 𝑛; 𝑏 ≥ 2, 𝑛 ∈ [0, 𝑏-1]

  An assignment 𝐴 matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • 𝑄 has 𝑖 right components identical to 𝑃’s, 𝑛 < 𝑖 ≤ 𝑏, and no other right components
  • The quantifier is replaced with an All quantifier

• ≥ 𝑛; b ≥ 2, n ∈ [1, 𝑏]

  An assignment 𝐴 matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • 𝑄 has 𝑖 right components identical to 𝑃’s, 𝑛 ≤ 𝑖 ≤ 𝑏, and no other right components
  • The quantifier is replaced with an All quantifier

• < 𝑛 (but more than 0); 𝑏 ≥ 2, 𝑛 ∈ [2, 𝑏]

  An assignment 𝐴 matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • 𝑄 has 𝑖 right components identical to 𝑃’s, 1 ≤ 𝑖 < 𝑛, and no other right components
  • The quantifier is replaced with an All quantifier

  and there is no assignment 𝐵 with a similar left component as 𝐴’s that matches pattern 𝑅 where

  • 𝑅’s left component is identical to 𝑃’s
  • 𝑅 has 𝑖 right components identical to 𝑃’s, 𝑖 ≥ 𝑛, and no other right components
  • The quantifier is replaced with an All quantifier

• ≤ 𝑛 (but more than 0); 𝑏 ≥ 2, 𝑛 ∈ [1, 𝑏]

  An assignment 𝐴 matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • 𝑄 has 𝑖 right components identical to 𝑃’s, 1 ≤ 𝑖 ≤ 𝑛, and no other right components
  • The quantifier is replaced with an All quantifier

  and there is no assignment 𝐵 with a similar left component as 𝐴’s that matches pattern 𝑅 where

  • 𝑅’s left component is identical to 𝑃’s
  • 𝑅 has 𝑖 right components identical to 𝑃’s, 𝑖 > 𝑛, and no other right components
  • The quantifier is replaced with an All quantifier

• ≠ 𝑛 (but more than 0); 𝑏 ≥ 2, 𝑛 ∈ [1, 𝑏]

  ≡ (< n) ∨ (> n)

• 𝑛1..𝑛2; 𝑏 ≥ 2, 𝑛_1_ ∈ [1, 𝑏], 𝑛_2_ ∈ [2, 𝑏], 𝑛_1_ < 𝑛_2_

  An assignment 𝐴 matches pattern 𝑃 if and only if it matches pattern 𝑄 where

  • 𝑄’s left component is identical to 𝑃’s
  • 𝑄 has 𝑖 right components identical to 𝑃’s, 𝑛_1_ ≤ 𝑖 ≤ 𝑛_2_, and no other right components
  • The quantifier is replaced with an All quantifier

  and there is no assignment 𝐵 with a similar left component as 𝐴’s that matches pattern 𝑅 where

  • 𝑅’s left component is identical to 𝑃’s
  • 𝑅 has 𝑖 right components identical to 𝑃’s, 𝑖 > 𝑛_2_, and no other right components
  • The quantifier is replaced with an All quantifier

• ∉ 𝑛1..𝑛2 (but more than 0); 𝑏 ≥ 4, n1 ∈ [2, b-1], n2 ∈ [3, 𝑏], 𝑛_1_ < 𝑛_2_

  ≡ (< 𝑛_1) ∨ (> 𝑛_2)

The order of the branches does not affect the evaluation result.

Q8: Any person born before 970 and passed away or whose father was born not later than January 1, 950 (two versions)

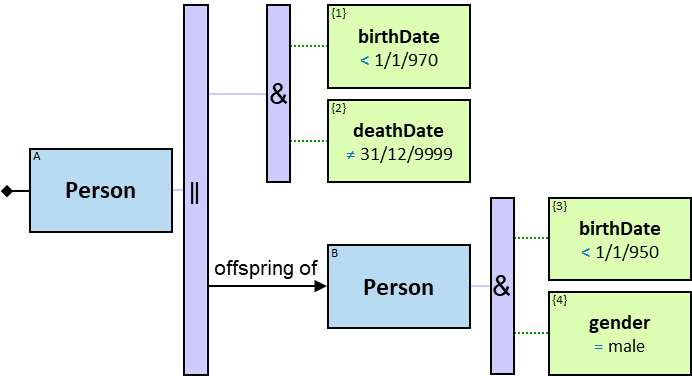
The person’s death date is not null, nor is it inapplicable. When A’s death date is null, ‘deathDate ≠ 31/12/9999’ is evaluated to unknown, and the constraint is not satisfied.

The following pattern also requires that A’s death date is not a future date:

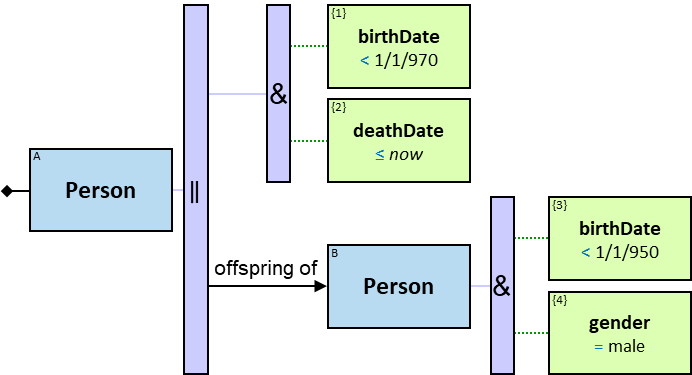
Q11: Any current member of the Masons Guild who, on or after January 1, 1011, befriended someone who had left the Saddlers guild or the Blacksmiths guild in June 1010 or later

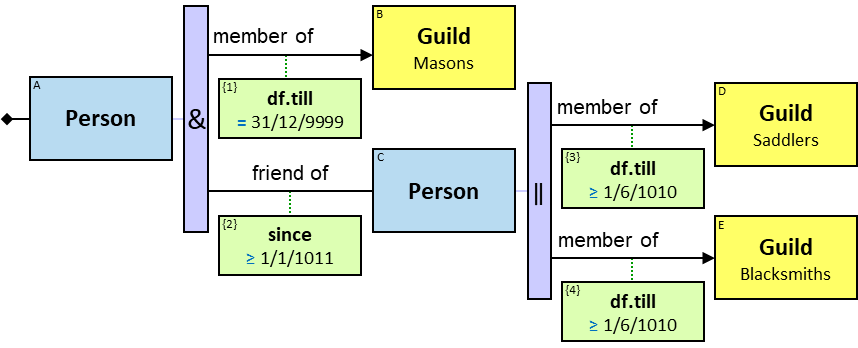
The constraint ‘member of df.till = 31/12/9999’ means an inapplicable membership end date – the person is currently a member of the Masons guild.

Entity-Tags

The letter in the top-left corner of each pattern-entity rectangle (concrete, typed, or untyped) is called an entity-tag. Entity-tags are also included in query results: any graph-entity in a query result is annotated with the same tag as the pattern-entity to which it was assigned so that the query poser can understand why any given entity is part of the result. As part of the result, a graph-entity may be annotated with more than one entity-tag, as it may be assigned to several pattern-entities (in the same assignment or in different assignments - when assignments are merged).

Entity-tags may be referenced:

• in identicality, nonidenticality, and order constraints
• in an aggregator per clause
• in an A1/M1/M2/M3 “et × et × …” clause
• in an M1 aggregator “with min/max …” clause (see Q196)

Identicality constraints can be used when the same graph-entity should be assigned to:

• Several typed entities of the same type
• Several untyped entities

Q4: Any person A whose dragon was frozen by a dragon owned by (at least) one of A’s parents

Entity-tag ‘B’ is used to enforce identical assignment to two Dragon pattern-entities.

Entity-tags with identicality constraints are depicted in green.

Q9: Any pair of dragons (A, B) where A froze B in both 980 and 984

The same visual notation is also used when the same concrete entity appears more than once (see Q25v2, Q26v2)

Nonidenticality constraint can be used when different graph-entities should be assigned to typed entities of the same type or to untyped entities.

Q5: Any person A whose dragon was frozen by a dragon owned by two of A’s parents (version 1)

Without the nonidenticality constraint, the same parent could be assigned to both D and E.

Nonidenticality constraints are depicted in red (‘≠X’), where X is another entity-tag. Several nonidenticality constraints may be defined for the same pattern-entity, e.g., ‘≠A,≠C’ (see Q57).

Q6: Any person A whose dragon was frozen by two dragons - one owned by one of A’s parents, the other owned by another parent (none, one, or both dragons may be owned by both parents)

Q7: Any person A whose dragon was either (i) frozen by a dragon owned by two of A’s parents or (ii) frozen by two dragons - one owned by one of A’s parents and the other owned by A’s other parent

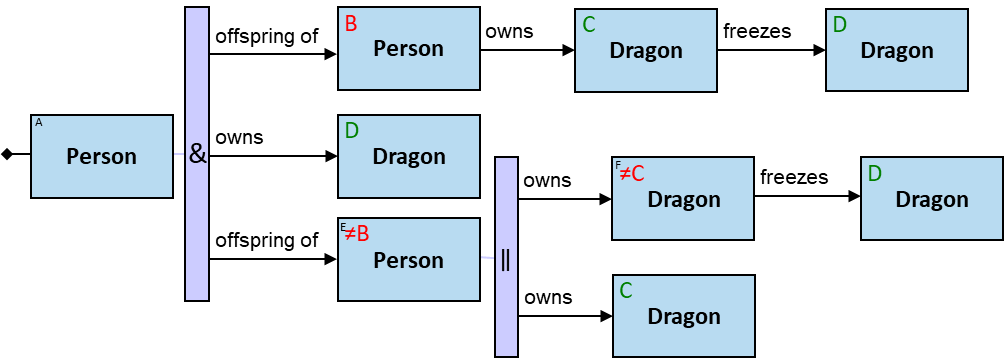
Q24: Any person A having (at least) two parents and owns a dragon that was frozen by a dragon neither of A’s parents owns

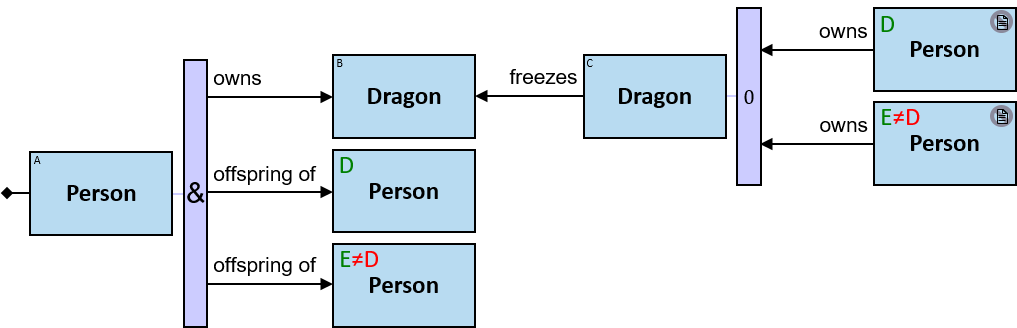
Q24 demonstrates the usage of both identicality and nonidenticality constraints for the same pattern-entity.

Consider Q5v1, Q6, Q7, and Q24. For any given assignment, there is another assignment where the two parents are switched (for example, in Q5v1, the assignments to D and E are switched). Such redundant assignments are usually undesired. Using order constraints, we can avoid such redundancies (see Q5v2).

Also, consider the following pattern: Any three persons A, B, and C, who are pairwise friends. If persons (A1, B1, C1) compose an assignment, so do (A1, C1, B1), (B1, A1, C1), and all other permutations. Such a factorial increase in the number of assignments is usually undesired. Using order constraints, we can express patterns such as Any three persons A<B<C, who are pairwise friends.

Order constraints can be used when graph-entities should be orderly assigned to either typed entities of the same type or untyped entities.

Q31: Any pair of dragons (A, B) where A froze B, A fired at B, B froze A, and B fired at A (version 1)

Without the order constraint, any reported pair of dragons would be reported twice: (D1, D2), (D2, D1).

Property graph data models usually require that each entity and relationship be uniquely identifiable. To support order constraints, V1 further requires that graph-entities would also be ordered.

Order constraints are depicted in red (‘<X’ or ‘≤X’), where X is another entity-tag. Several nonidenticality or order constraints may be defined for the same pattern-entity, e.g., ‘<A,<B’, ‘≠A,<C’ (see Q83).

See also Q49, Q88, Q115v1, Q272, Q337, Q342, Q347, and Q350.

If, for some assignment, an identicality, nonidenticality, or order constraint is not relevant (e.g., identicality constraint between a pair of entities in two branches of a Some quantifier, where the assignment includes only one branch) - the constraint is ignored. Otherwise - the assignment is valid only if the constraint is satisfied.

Negator

Sometimes we need to express a pattern containing elements for which there is no assignment. For example, any person whose first name is Brandon and who does not own a white horse. Such patterns are composed of:

• A ‘positive’ component - any person whose first name is Brandon
• A negator - does not
• One or more ‘negative’ components - own a white horse

An assignment matches the pattern only if:

• It matches a pattern composed only of the positive component: there is an assignment to a person whose first name is Brandon.
• The assignment has no superset that matches a pattern composed of the positive component and the negative components: the person whose first name is Brandon does not own a white horse.

Such patterns can be composed using negators. The pattern starts with the ‘positive’ component, and negators separate it from the ‘negative’ components.

A negator is depicted by a narrow pink ‘X’ rectangle. The rectangle has one on its left side and one on its right side.

On its left, there is either

• an entity
• a quantifier (see Q20v1)

On its right is a relationship or a path (see Paths, Q84)

• optionally, with a relationship/path-negator (see Relationship/Path-Negator, Q82v1)
• optionally, with relationship’s expressions (see Q99v1)
• with no ‘O’ (see Optional Components)
• with no aggregators (see Aggregators)

Query results do not include assignments to entities/relationships/paths right of a negator. Any pattern entity right of a negator is depicted with a gray ‘no report’ icon on its top-right, indicating that the query result does not include its assignment (see Latent pattern-entities).

Q12: Any person who does not own a horse

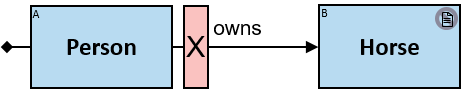
Q13: Any horse not owned by a person

Q14: Sweetfoot - if no person owns it

Q15: Brandon Stark - if he does not own a horse

Q16: Any person who does not own Sweetfoot

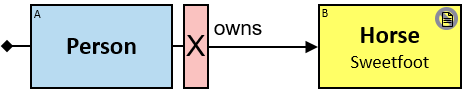
Q17: Any horse not owned by Brandon Stark

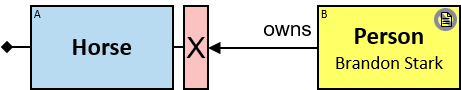
Q18: Brandon Stark - if he does not own Sweetfoot

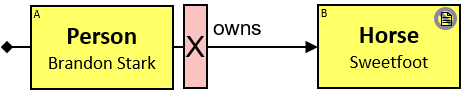
Q19: Sweetfoot - if Brandon Stark does not own it

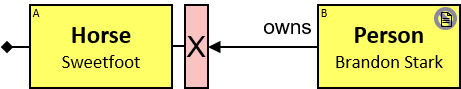
Q256: Any person who does not own a white horse

Q257: Any person who did not become a horse owner in or after 1011

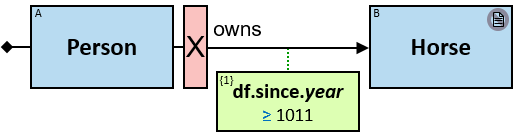
Q258: Any person who did not become a white horse owner in or after 1011

Q22: Any horse not owned by a person who owns a dragon

The positive component is a horse, while the negative component is owned by a person who owns a dragon. The right component is anything that follows the negator - up to the end of the branch.

Valid assignments:

• Any horse that is not owned
• Any horse that none of its owners is a person (e.g., a horse owned by a guild)
• Any horse that each person who owns it - does not own a dragon

Q333: Any person who does not own a dragon that both fired at and froze the same dragon

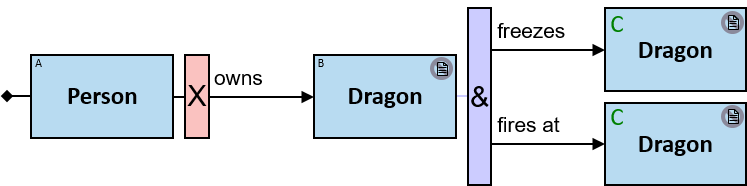
A negator may also appear left of a relationship that directly follows a quantifier’s branch:

Q25: Any dragon (C) not fired at by Balerion but fired at by a dragon that Balerion fired at (two versions)

Q26: Any person who is a member of at least one guild that Brandon Stark is a member of and at least one guild that Brandon Stark is not a member of (four versions)

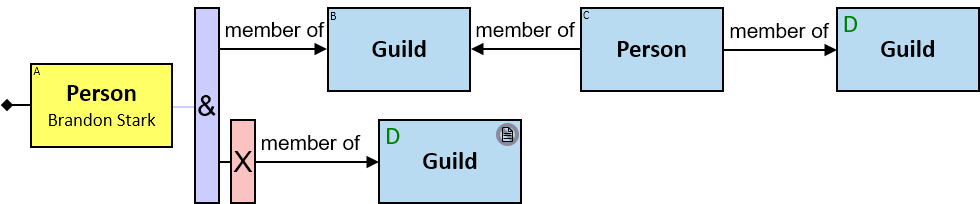
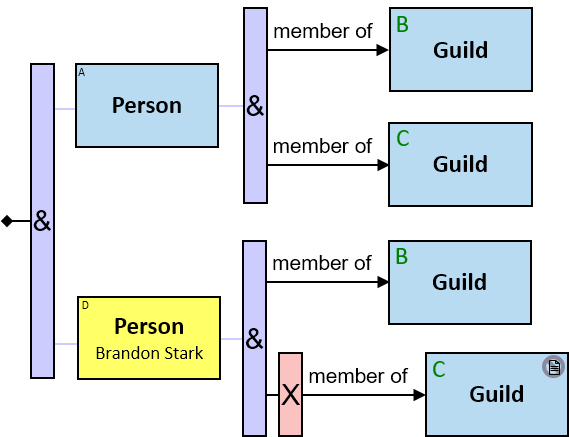
Negators may appear in more than one branch:

Q20: Any horse neither owned by Rogar Bolton nor by Robin Arryn (two versions)

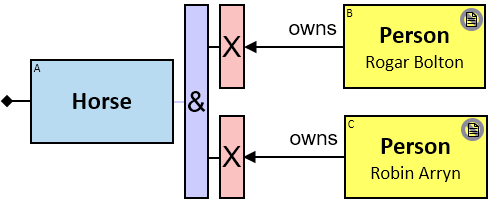
Note that there are two negative components. This query can also be represented using the None quantifier:

Q21: Any horse not owned by both Rogar Bolton and Robin Arryn

If either Rogar Bolton or Robin Arryn owns the horse - the owner will not be part of the reported assignments.

Q362: Any horse owned either by Rogar Bolton or Robin Arryn but not by both

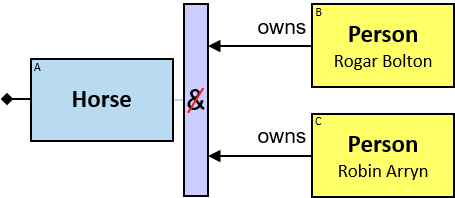
If either Rogar Bolton or Robin Arryn owns the horse - the owner will be part of the reported assignments.

Negators may also appear in a sequence:

Q23: Any horse not owned by a person who does not own a dragon

The positive component is a horse, while the negative component is owned by a person who does not own a dragon. The right component is anything that follows the left negator - up to the end of the branch.

Valid assignments:

• Any horse that is not owned
• Any horse that none of its owners is a person (e.g., a horse owned by a guild)
• Any horse that each person who owns it - also owns a dragon

EA-tags, entity type-tags, and relationship type-tags defined right of a negator can only be referenced right of that negator.

Identicality, nonidenticality, and order constraints cannot be defined between pattern-entities in different negative components.

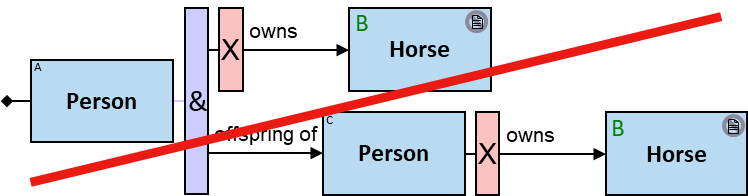
Relationship/Path-Negator

The pattern Any person whose first name is Brandon and who does not own a white horse has assignments in two cases:

• There is a person whose first name is Brandon, and there are no white horses
• There is a person whose first name is Brandon, and there is at least one white horse, but there is no person whose first name is Brandon who owns a white horse

Sometimes we want an assignment to match the pattern only in the second case - we want only assignments that match the whole pattern except for given relationships/paths. Hence, an assignment matches the pattern only if:

• It matches a pattern composed of the left component and the right component without the relationship/path
  • There is a person whose first name is Brandon
  • There is a white horse
• The assignment has no superset that matches a pattern composed of the left component, the right components, and the relationship/path
  • There is no person whose first name is Brandon who owns a white horse

A relationship/path-negator is depicted with a red ‘✕’ at the center of the relationship/path arrow/line. The arrow/line and the associated text are faded.

A component located right of a pattern relationship/path with a relationship/path-negator is required to have an assignment. Such assignments are included in the reported pattern assignment. The relationship/path is reported as a negated relationship/path, which may have a type and properties.

Q357: Any dragon for which there is at least one dragon (besides itself) it did not freeze

Each assignment comprises a dragon, a negated freezes relationship, and a dragon it did not freeze.

Q83: Any dragon for which there are at least two dragons (besides itself) it did not freeze

Q204: Any dragon for which there is a dragon not owned by a Sarnorian that did not freeze it

Q205: Any dragon A and Sarnorian subject C where there is a dragon not owned by C that did not freeze A

Relationship/path-negators are often used with aggregators (see Q126, Q63-Q66, Q165, Q298, Q345).

A relationship/path with a relationship/path-negator may be wrapped with a negator.

Q82: Any dragon that froze all other dragons. Alternative phrasing: Any dragon for which there is no dragon (besides itself) it did not freeze (version 1)

Combiner

A combiner combines two or more consecutive branches of the same quantifier.

A combiner is depicted by a narrow purple ‘}’ rectangle. The rectangle has one connection on its left side and one on its right side.

On its left, there can be

• Types relationships, untyped relationships (see Q53), and paths
  • optionally, with a negator (see Q35) or with an ‘O’
  • optionally, with a relationship/path-negator (see Q360v2)
  • optionally, with relationship’s expressions (see Q185)
  • optionally, with aggregators (see Q244)
• a combiner (see Q100)

On its right – there is either

• an entity
• a combiner (see Q100)

The entity-type on a combiner’s right side must match all the relationship-types and paths on its left side.

Q30: Any pair of dragons (A, B) where A both froze B and fired at B (two versions)

A combiner is syntactic sugar, which, alternatively, can be implemented by duplicating anything right of it to each branch.

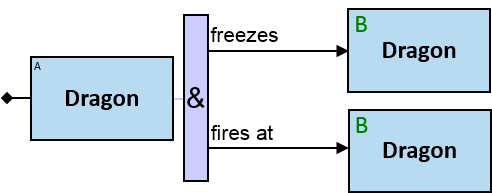
Q187: Any dragon Balerion froze at least once on or after January 1, 1010, and at least once for less than ten minutes

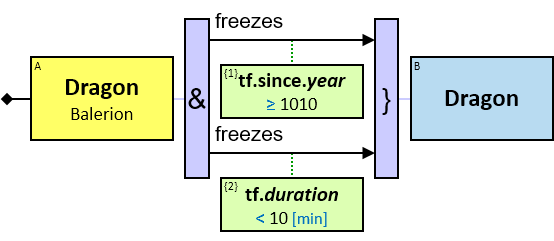
Note that the same graph-relationship may be assigned to both freezes pattern-relationships. Compare with Q185.

Q189: Any dragon Balerion froze at least once on or after January 1, 1010, or at least once for less than ten minutes

Q29: Any dragon that froze or fired at some dragon (versions 1-3)

Note that the implied identicality is redundant.

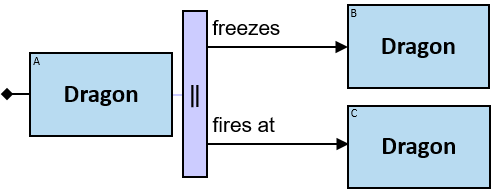
See also note under Q121v1 - combiner right of an A1 aggregator.

Q31: Any pair of dragons (A, B) where A froze B, A fired at B, B froze A, and B fired at A (version 2)

Without the order constraint, any reported pair of dragons would be reported twice: (D1, D2), (D2, D1).

Q32: Any pair of dragons (A, B) where A fired at both B and some dragon that fired at B

Q5: Any person A whose dragon was frozen by a dragon owned by two of A’s parents (version 2)

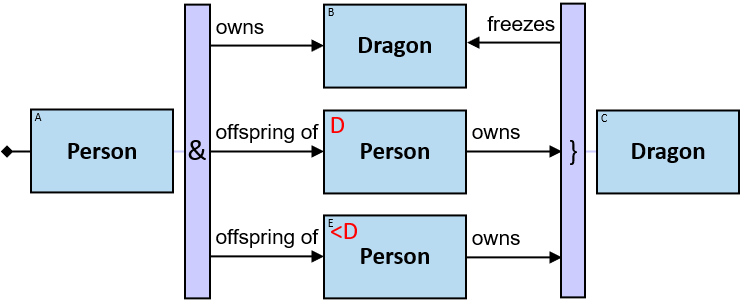
Q170: Any three dragons (A, B, D) where A fired at B, A fired at some dragon that fired at B, B froze D, and B froze some dragon that froze D

Q33: Any dragon A that froze some dragon B, froze some dragon that froze B, and fired at some dragon

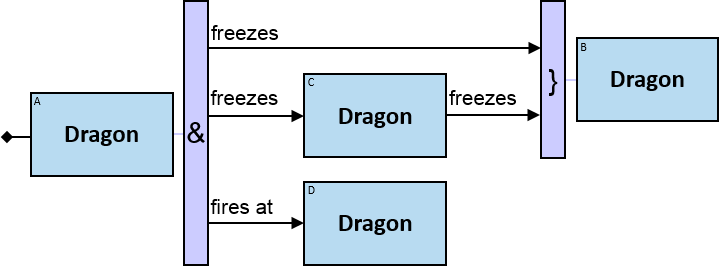
Different branches may be combined with different combiners.

Q34: Any dragon A that froze some dragon B, froze some dragon that froze B, fired at some dragon D, and fired at some dragon that fired at D (B and D may be the same dragon or different dragons)

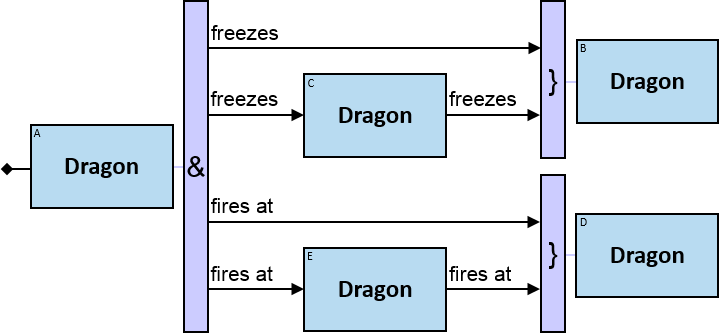
Q35: Any pair of dragons (A, B) where A froze B but did not fire at B

At least one combined branch must be a non-negative component.

For the None quantifier, all the branches are negative components.

Chains, Horizontal Quantifiers, and Horizontal Combiner

Relationship’s expressions can be chained. When chained, each expression with a constraint is a filtering stage. An assignment is valid only if all the chained constraints are satisfied, or in other words - if it passes all filtering stages.

Q188: Any dragon Balerion froze at least once - on or after January 1, 1010, for less than ten minutes

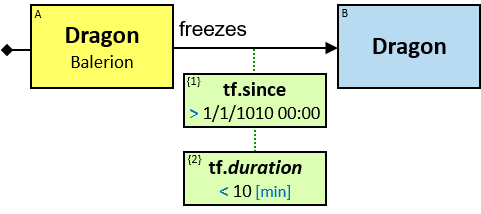
Q10: Any person whose first name is Brandon, who owns some dragon B which froze a dragon C that (i) belongs to an offspring of Rogar Bolton, and (ii) froze a dragon that belongs to either Robin Arryn or Arrec Durrandon. B froze C at least once in or after 1010 - for longer than 100 seconds

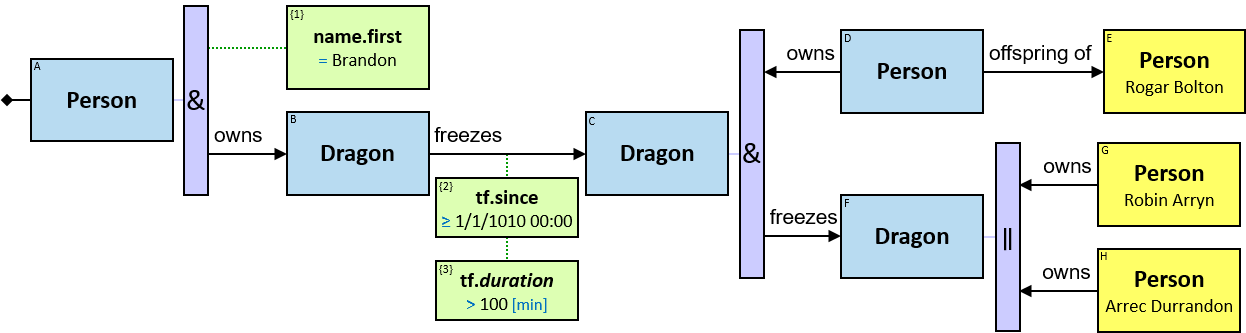
A horizontal purple rectangle represents a horizontal quantifier. The text inside the rectangle denotes the quantifier type.

Eleven horizontal quantifier types are defined (as for vertical quantifiers, except the All quantifier). Their semantics are similar to those of vertical quantifiers. All can be implemented by chaining relationship’s expressions or by using vertical quantifiers (see Q100).

On the top of a horizontal quantifier, there can be

• a relationship (see Q300)
• a relationship’s expression (see Q301v1)
• a horizontal quantifier

On its bottom, there are zero or more branches. Each branch starts with either

• a relationship’s expression (see Q267v3)
• a horizontal quantifier

A branch composed of relationship’s expressions with no constraints does not affect the quantifier’s evaluation.

A horizontal combiner may be used to combine two or more consecutive branches of the same horizontal quantifier. Each branch ends with either

• A relationship’s expressions (see Q302)
• A horizontal combiner

Below a horizontal combiner, there can be either

• Another chained stage that starts with
  • a relationship’s expression (see Q301v2)
  • an aggregator (see Q302)
  • a horizontal quantifier
• A horizontal combiner

Q300: Any pair of dragons (A, B) where A froze B, and at least two of the following conditions are satisfied: (i) the freeze duration was longer than ten minutes, (ii) the freeze started after January 1, 980, and (iii) the freeze ended before February 1, 980

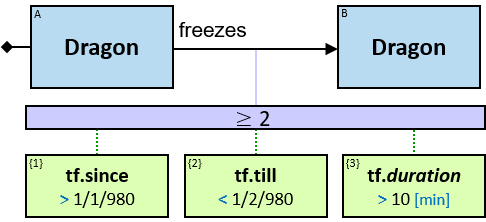
Q301: Any pair of dragons (A, B) where A froze B for more than ten minutes, and either the freeze started after January 1, 980, or the freeze ended before February 1, 980 (two versions)

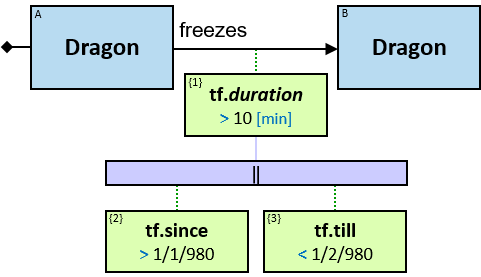
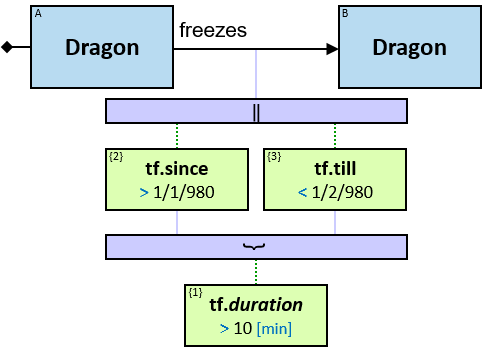
See also Q267v3.

Latent Pattern-Entities

Pattern entities may be annotated as implicit latent or explicit latent.

Assignments to latent pattern-entities and assignments to pattern-relationships and pattern-paths connected to latent pattern-entities are not included when pattern assignment is reported.

Implicit latent pattern-entities are pattern-entities that appear

• right of a negator (see Q12, Q22, Q288)
• right of a None quantifier, except branches (or subbranch of a sequence of quantifiers that follows the None quantifier) that starts with an ‘O’ (see Q359)

Such typed and untyped entities are required to have no assignments; hence, trivially, no assignments would be reported. Such concrete entities would not be reported as well (see Q20).

Implicit latent pattern-entities are depicted with a gray ‘no report’ icon on their top-right. These icons are automatically added by the interactive pattern-builder/visualizer tool and may not be added/removed by the pattern composer.

An entity right of a combiner is not depicted as implicit latent even if it is implicit latent according to one or more branches (see Q35).

Explicit latent pattern-entities are non-implicit latent pattern-entities, which the pattern composer marks as latent. Though they may have assignments - those assignments are required not to be reported. Any non-implicit latent pattern-entity may be set as explicit latent.

Explicit latent pattern-entities are depicted with a red ‘no report’ icon on their top-right.

Q142: Any person who owns a white or a black horse and has a parent who owns a dragon. The parent and its dragon are not to be included in the reported assignment

Suppose person A1 has two parents, each with four owns relationships to dragons. Without the latent annotations, there would be eight pattern assignments per person and owns relationship to a horse. With the latent annotations, there would be only one assignment per person and owns relationship to a horse.

Q143: Any person who owns a horse that is neither white nor black and has a parent that does not own a horse. The parent is not to be included in the reported assignment

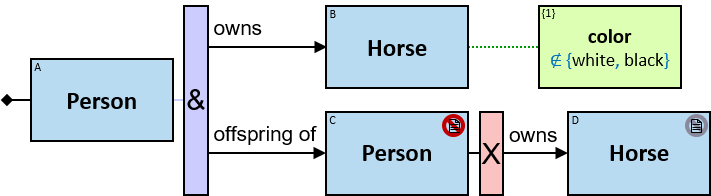
When several pattern-entities have the same entity-tag, some may be latent (implicit or explicit) while others are not. See Q337, Q339.

Concrete, typed, and untyped entities may all be latent - implicit or explicit.

At least one pattern-entity should be non-latent.

Optional Components

Anything right of an optional is optional: if it has a valid assignment - it will be reported (unless it is latent). Otherwise - it will not.

An optional (i.e., an ‘O’) is depicted with a magenta ‘O’ rectangle. The rectangle has one connection on its left side and one on its right side.

On its left, there is either

• an entity
• a quantifier (see Q144), except a quantifier at the start of the pattern

On its right, there is either

• a relationship or a path (see Paths)
  • with no negator
  • optionally, with a relationship/path-negator (see Q126)
  • optionally, with relationship’s expressions (see Q339)
  • optionally, with aggregators (see Q125)
• a quantifier
  • optionally, with aggregators (see Q360v2)

Alternatively:

On its left is a quantifier at the start of the pattern, and on its right is an entity (see Q321v1)

Q147: Any person A. If A owns both a horse and a dragon - they should be included in the assignment

Q149: Any person A. If A owns a horse - it should be included in the assignment. If A owns a dragon - it should be included in the assignment as well

Q81: Balerion. If there is a dragon it did not freeze - it should be included in the assignment

Quantifier’s branches that start with an ‘O’ do not affect the quantifier’s evaluation.

Assignments to optional branches are reported regardless of the quantifier type, but only when there is an assignment to the pattern.

Q144: Any person A who owns a white horse. If A has a parent who owns a horse - the parent and its horse should be included in the assignment

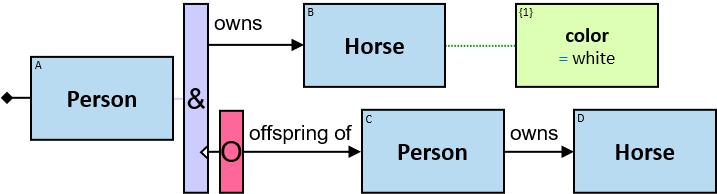
Q145: Any person A who owns a white horse. If A has a parent that does not own a horse - the parent should be included in the assignment

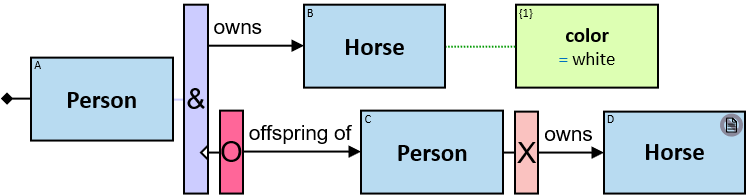
Q146: Any person A who owns a white horse. If A has a parent - the parent should be included in the assignment. If A’s parent owns a horse - this horse should be included in the assignment as well

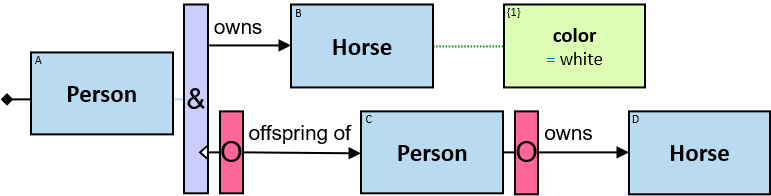
Q148: Any person A who owns both a horse and a dragon. If A has a parent - the parent should be included in the assignment

Q150: Any person A who owns a horse or a dragon. If A has a parent - the parent should be included in the assignment

Q203: Any person A. If A owns both a horse and a dragon - they should be included in the assignment. If A owns both a horse and a dragon and also has a parent - the parent should be included in the assignment as well

Q359: Any dragon A where (i) there is no black dragon A froze, (ii) there is no white dragon A did not freeze, (iii) there is at least one gold dragon A froze, and (iv) there is at least one silver dragon A did not freeze. Also, report any red dragon that A froze and any blue dragon that A did not freeze

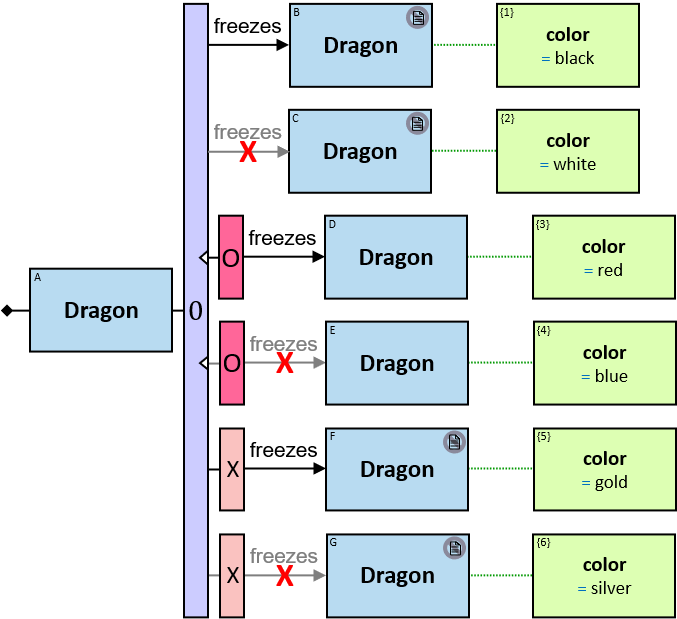
When tags right of an ‘O’ have no assignments:

• An expression-tag defined right of an ‘O’ is evaluated to null (see Q140, Q141)
• An A1/A2 aggregation-tag defined right of an ‘O’ is evaluated to zero (see Q125, Q347, Q259v2)
• An A3 aggregation-tag defined right of an ‘O’ is
  • evaluated to null when aggop is min/max/avg (see Q317)
  • evaluated to zero when aggop is sum/distinct (see Q320v2, Q321v2)
  • evaluated to {} / [] when aggop is set/bag/union/intersection (see Q318)

Entity-tags defined right of an ‘O’ cannot be used in identicality, nonidenticality, and order constraints defined left of the ‘O’.

Entity type-tags, defined right of an ‘O’ cannot be used in entity-type constraints defined left of the ‘O’.

Relationship type-tags defined right of an ‘O’ cannot be used in relationship-type constraints defined left of the ‘O’.

Entity-tags, entity type-tags, and relationship type-tags defined right of an ‘O’ can be used in aggregators defined left of the ‘O’:

• A/M/R aggregators: 𝑇 may contain tags defined right of an ‘O’
• A1/A3/M aggregators: 𝐵 may contain tags defined right of an ‘O’ (see Q295, Q320, Q321v1)
• M1 aggregator: 𝑀 may contain tags defined right of an ‘O’

Untyped Entities

A relationship-type may hold between different pairs of entity-types (e.g., owns: {(Person, Dragon), (Guild, Dragon), (Null, Dragon)}). Untyped entities can be used to express patterns such as Any dragon and its owners, where the owner can be either a person, a guild, or Null.

A red rectangle represents an untyped entity. Graph-entities of different types may be assigned to an untyped entity.

A red rectangle containing only an entity-tag represents an entity with no explicit entity-type constraint.

Q36: Any person who owns something

B assignments are implicitly type-constrained to things that a person can own.

Implicit entity-type constraints are inferred from the pattern, including from identicality, nonidenticality and order constraints.

Q49: Any three dragons with a cyclic freeze pattern and their owners (if any)

The entity-types of all owners are implicitly constrained to things that can own a dragon.

Entities are implicitly type-constrained also when untyped entities are on either side of a negator or a relationship-negator:

Q39: Any entity of a type that can own a dragon but does not

Q40: Any dragon that is not owned

Q41: Any entity of a type that can be owned but is not owned

Q42: Any entity of a type that can own something but owns nothing

In addition to the implicit entity-type constraints, explicit entity-type constraints can be enforced using:

• a type equality constraint (‘= ⟨ ett ⟩’) (see Q50),
• a type inequality constraint (‘≠ entity-type’ (see Q43) or ‘≠ ⟨ ett ⟩’ (see Q51))
• a set of at least two allowed entity-types and/or type-tags (‘∈ {…}’) (see Q37), or
• a set of at least two disallowed entity-types and/or type-tags (‘∉ {…}’) (see Q52)

Q43: Any dragon that all of its owners (if any) are people

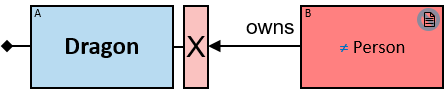
Q37: Any person who owns a horse or a dragon

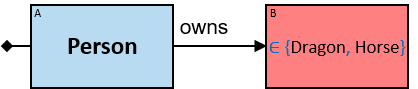
Q38: Any person who owns something which is neither a horse nor a dragon

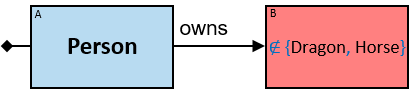
For each untyped entity, implicit and explicit type constraints must not nullify the list of valid entity-types. Explicit type constraints must not contradict implicit type constraints. This can be asserted during query analysis.

Since both horse and dragon entity-types have a name property of the same data type (string) - the following pattern is valid:

Q291: Any person who owns a horse or a dragon whose name starts with an ‘M’

Entity Type-Tags

A red rectangle (denoting an untyped entity) may contain an entity type-tag, depicted by a numeric index wrapped in angle brackets. An entity type-tag represents the entity-type of the entity in a given assignment.

Entity type-tags may be referenced:

• in a type constraint of an untyped entity (see Q50, Q52)
• in an extended aggregator per clause (see Q218v2, Q350)
• in an A3 aggregator “aggop …” clause (see Q167v2)
• in an extended M1/M2/M3 aggregator “[all but] 𝑘 …” clause (see Q209, Q210)

Q50: Any person who owns (at least) two things of the same type

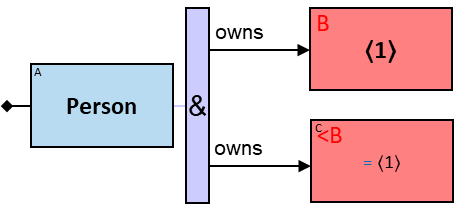
Q51: Any person who owns (at least) two things of different types

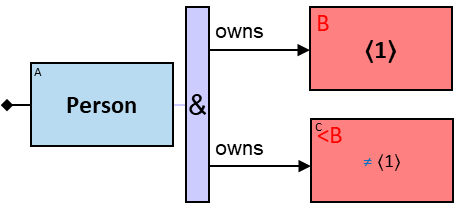
Q52: Any person who owns (at least) two things of different types, neither is a horse

Q167: Any person whose owned entities are all of the same type (version 1)

For any quantifier except All - an entity type-tag defined in a branch can only be referenced in that branch.

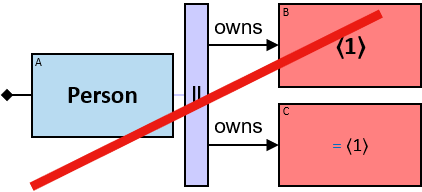
An entity type-tag defined right of a negator can only be referenced right of that negator.

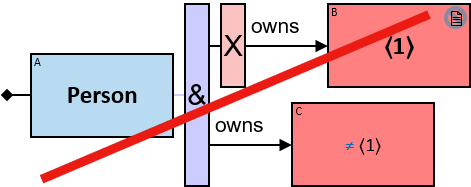
An entity type-tag defined right of an ‘O’ can only be referenced right of that ‘O’, except when used in an aggregator’s 𝑇 (any aggregator) or 𝑀 (A3, M1, M2, M3 aggregators) definition.

Untyped Relationships

Multiple relationship-types may hold between a pair of entity-types (e.g., freezes: {(Dragon, Dragon)}, fires at: {(Dragon, Dragon)}. Untyped relationships can be used to express patterns such as Any pair of dragons with at least one relationship, where the relationship-type can be either freezes or fires at.

A red arrow/line with no type label or with type constraints represents an untyped relationship. Graph-relationships of different types may be assigned to an untyped relationship.

A red arrow/line with no label represents a relationship with no explicit type constraints:

Q29: Any dragon that froze or fired at some dragon (version 4)

The relationship is implicitly type-constrained to directional relationship-types between two dragons.

Q53: Any person with a path of length up to three to Rogar Bolton (version 1)

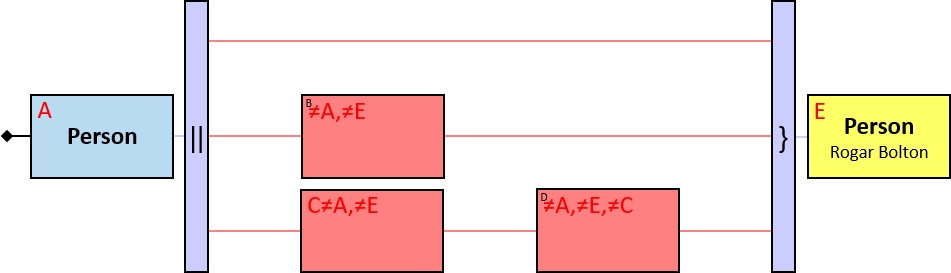
Relationships are implicitly type-constrained also when a negator or a relationship-negator wraps an untyped relationship:

Q360: Any dragon that (froze or fired at) all other dragons. Alternative phrasing: Any dragon for which there is no dragon (besides itself) it did not (freeze or fire at) (version 1)

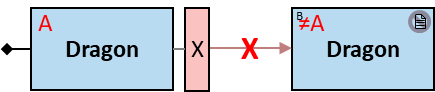
In addition to the implicit relationship-type constraints, explicit relationship-type constraints can be enforced using:

• a type equality constraint (‘= ⟪ rtt ⟫’) (see Q367),
• a type inequality constraint (‘≠ relationship-type’ (see Q364) or ‘≠ ⟪ rtt ⟫’ (see Q365))
• a set of at least two allowed relationship-types and/or type-tags (‘∈ {…}’) (see Q121v2), or
• a set of at least two disallowed relationship-types and/or type-tags (‘∉ {…}’) (see Q368)

Q364: Any person and an entity that have a relationship of a type other than ‘friend of’

Implicit relationship-type constraints are inferred from the pattern (including from relationships directionality and from entities identicality/nonidenticality/order constraints).

For each untyped relationship, implicit and explicit type constraints must not nullify the list of valid relationship-types. Explicit type constraints must not contradict implicit type constraints. This can be asserted during query analysis.

Relationship Type-Tags

Instead of a relationship-type, a relationship label may denote a relationship type-tag, depicted by a numeric index wrapped in double angle brackets. A relationship type-tag represents the relationship-type of the relationship in a given assignment.

Relationship type-tags may be referenced:

• in a type constraint of an untyped relationship (see Q365)
• in an extended aggregator per clause (see Q369)
• in an A3 aggregator “aggop …” clause (see Q366v2)
• in an extended M1/M2/M3 aggregator “[all but] 𝑘 …” clause (see Q369)

Q365: Any pair of dragons that have relationships of at least two types

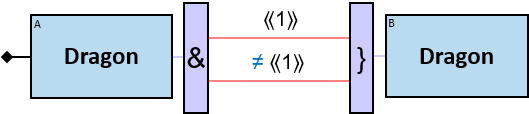
Q366: Any pair of dragons that have relationships of at least three types (version 1)

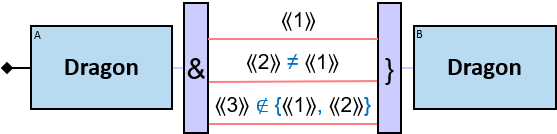
Since there are only two relationship-types between a pair of dragons (freezes, fires at), this pattern would never have assignments. This can be detected during query analysis.

Q367: Any pair of dragons that have a directional relationship of the same type in both directions

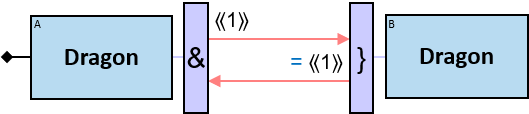
Q368: Any pair of dragons that have relationships of at least two types, neither is ‘freezes’

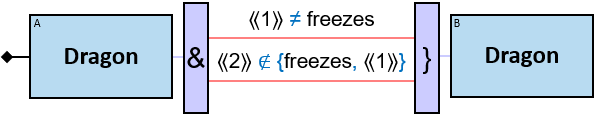
Again, the fact that this pattern would never have assignments can be detected during query analysis.

For any quantifier except All - a relationship type-tag defined in a branch can only be referenced in that branch.

A relationship type-tag defined right of a negator can only be referenced right of that negator.

A relationship type-tag defined right of an ‘O’ can only be referenced right of that ‘O’, except when used in an aggregator’s 𝑇 (any aggregator) or 𝑀 (A3, M1, M2, M3 aggregators) definition.

Null Entities

As described above, graph-entities of type Null realize action-types and relationships to unknown/unimportant entities.

Since each graph-entity of type Null is connected by exactly one relationship, there are additional implicit constraints on each typed entity of type Null and on each untyped entity that explicitly allows type Null:

• There is no relationship/path on its right (it is a terminal node), or there is no relationship/path on its left (it starts the pattern)
• It is not directly right of a combiner nor directly left of a quantifier
• It is not being aggregated
• Its single connection is either a relationship of a type that supports Null entities on this side or a path that may end with such a relationship
• Its entity-tag is not reused (no identicality, nonidenticality, or order constraints)

As part of a pattern:

• Concrete entities may not be of type Null
• Typed entities may be of type Null if there are no implicit type constraints that disallow it
• For untyped entities, type Null may be explicitly allowed or disallowed only when there are no implicit type constraints that disallow it

As part of an assignment:

• For an untyped entity - graph entities of type Null are valid assignments only if
  • There are no implicit type constraints that disallow it, and
  • There are no explicit type constraints that disallow it, or there are explicit type constraints that allow it

See G1-G20.

Paths

A graph-path is a sequence of graph-entities and graph-relationships that starts with a graph-entity and ends with a graph entity. A simple graph-path is a graph-path where all entities are pairwise distinct, except, possibly, the first and last.

Each graph-path has a length. The path length is equal to the number of graph-relationships along the path; hence, a relationship is a path of length 1.

A pattern-path connects two pattern-entities - like a pattern-relationship. However, while a pattern-relationships are assigned with graph-relationships, pattern-paths are assigned with simple graph-paths minus the first and last entities, which are not considered a part of the assignment. Thus, pattern-paths are assigned with at least one graph-relationship.

A blue line between two pattern-entities represents a pattern-path. Above the line is a constraint on the path length. An upper bound on the path length must be defined, hence the constraint must be defined using one of the following constraint types: = expr, < expr, ≤ expr, in set-expr, in bag-expr, in list-expr, or in interval-expr, where all expressions or interval bounds evaluate to positive integers.

Q53: Any person with a path of length up to three to Rogar Bolton (version 2)

Q84: Any dragon with no paths of length up to three to other dragons

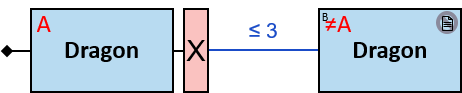
Q55: Any entity with paths of length up to three to Rogar Bolton, Robin Arryn, and Arrec Durrandon

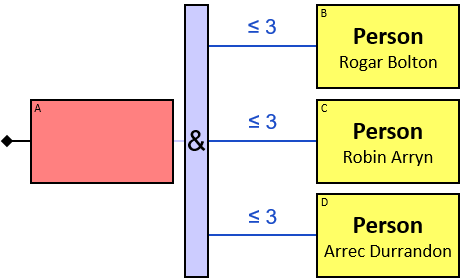
Constraints may be defined for both the entities and the relationships along the path:

Constraints on relationships along the path are listed in blue curly brackets above the path’s line. The brackets may list either:

• Allowed relationship-types - e.g., {fires at, freezes}. Any unlisted relationship-type is disallowed.
• Constraints on the number of relationships of given types, with optionally - a given direction - e.g., {freezes < 2, fires at = 2}, {freezes = 0}, {→ freezes = 2, ← freezes = 1}. Any unlisted relationship-type / direction is allowed.

Constraints on entities along the path are listed in blue curly brackets below the path’s line. The brackets may list either:

• Allowed entity-types - e.g., {Dragon}, {Dragon, Horse}. Any unlisted entity-type is disallowed.
• Constraint on the number of entities of given types - e.g., {Dragon = 0}, {Dragon ≥ 1, Horse ≥ 1}. Any unlisted entity-type is allowed.

A path cannot be composed of Null entities since they are terminal nodes. Therefore, the list of allowed entity-types may not contain Null. Similarly, the list of disallowed entity-types may not contain Null as it is implicitly disallowed.

Q44: Any path of length up to four between Vhagar and Balerion, which is composed only of ‘freezes’ relationships

Q45: Any path of length up to four between Vhagar and Balerion composed only of ‘freezes’ and ‘fired at’ relationships

Q46: Any path of length up to four between a dragon owned by Rogar Bolton to a dragon owned by Robin Arryn, which is composed of up to two ‘freezes’ relationships and only of ‘Dragon’ entities

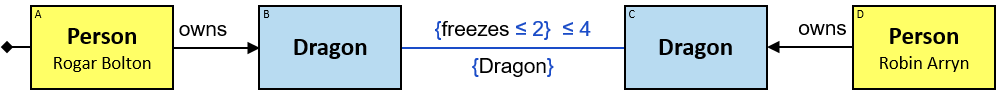
Q54: Any person with paths of length up to three to Rogar Bolton, Robin Arryn, and Arrec Durrandon. The paths composed only of ‘friend of’ relationships

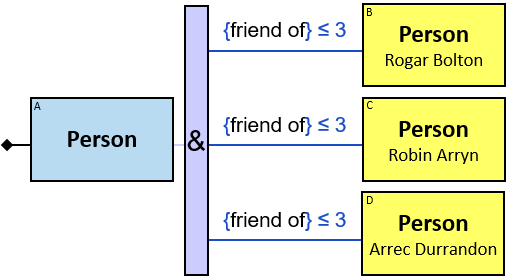
Shortest Paths

Instead, or in addition to specifying a constraint on the path length - a shortest path constraint can limit paths-assignments to the shortest ones that subject to the constraints on the entities/relationships along the path. If, for example, the length of the shortest path that subjects to the constraints is three - only paths of length three are valid assignments.

Q47: All shortest paths between Vhagar and Balerion

Q48: All shortest paths between Vhagar and Balerion, which are neither composed of ‘freezes’ relationships nor ‘Dragon’ entities (version 1)

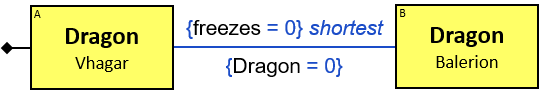
shortest may not appear directly right of a negator or a path-negator.

Path Patterns

An alternative to constraints on the entity-types and the relationship-types along a path are constraints on the subgraphs which assignments to a path are composed of.

A path pattern is a pattern that has one entity marked as left-terminal and one entity, possibly the same one, marked as right-terminal.

A path-assignment is composed of chained subgraphs; each subgraph is assigned to a path pattern. There is an overlap between assignments to successive path patterns:

• The graph-entity assigned to the left-terminal of the first path pattern of a path is also assigned to the entity preceding the path
• The graph-entity assigned to a right-terminal of a path pattern is also assigned to the left-terminal of the successive path pattern
• The graph-entity assigned to the right-terminal of the last path pattern of a path is also assigned to the entity following the path

A blue table below the path defines constraints on the path’s path pattern types. The table has two columns:

• A constraint on the number of allowed path pattern instances of this type along the path. The following constraint types can be used: n, <n, ≤n, >n, ≥n, n₁..n₂, where the values are positive integer constants.
• A path pattern

The last row defines whether a path-assignment may be composed of other graph-elements (‘✔’ if yes, ‘✘’ if no).

Q48: All shortest paths between Vhagar and Balerion, which are neither composed of ‘freezes’ relationships nor ‘Dragon’ entities (version 2)

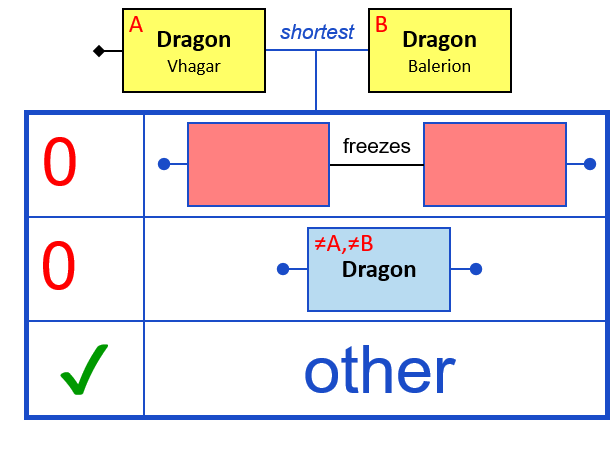
Q58: Any Sarnorian who has a path of length up to six to an Omberian. The path passes through Rogar Bolton

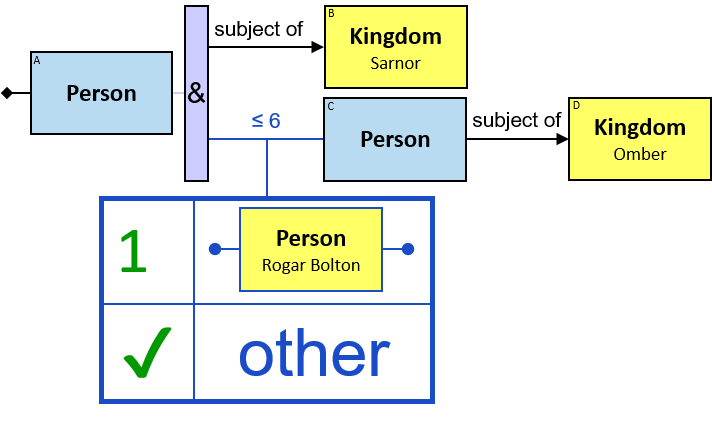
Q56: constraints on path patterns

In this example, path assignments must be composed of assignments to four path patterns

Q57: constraints on path patterns

• Path assignments must not contain people whose first name starts with ‘M’ (note that assignments to A and C are not considered part of the path assignment)
• There must be between two and three assignments to any of two path patterns
• The path may be composed of additional graph-elements

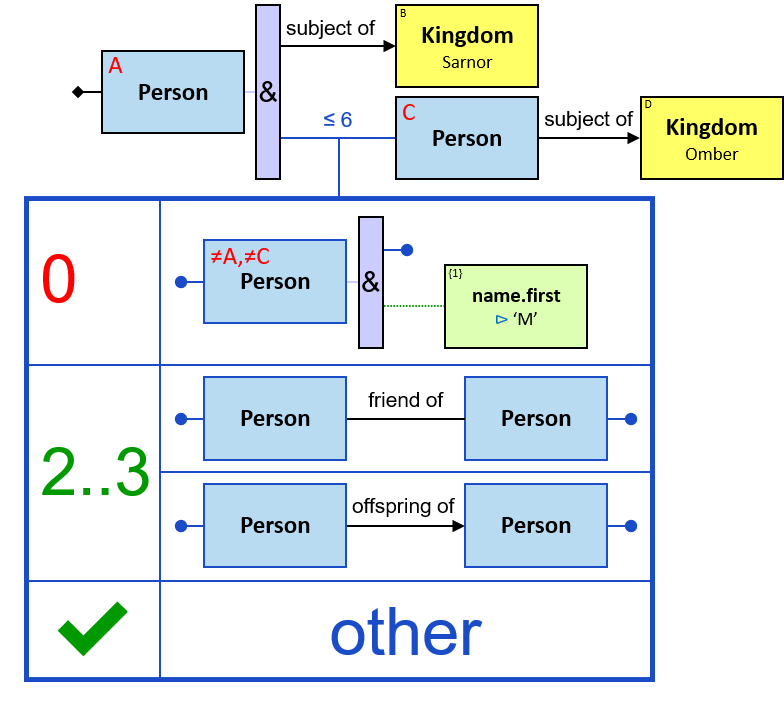
Q322: Any dragon owned by at least five consecutive generations of the same dynasty

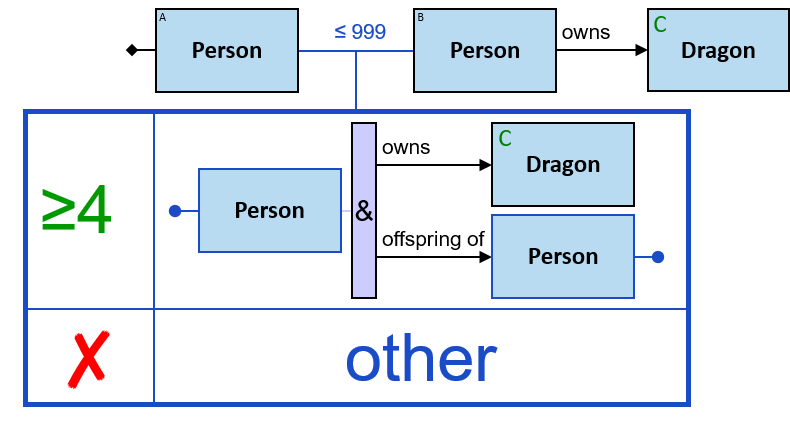
Q323: Any dragon owned by at least five (not necessarily consecutive) generations of the same dynasty

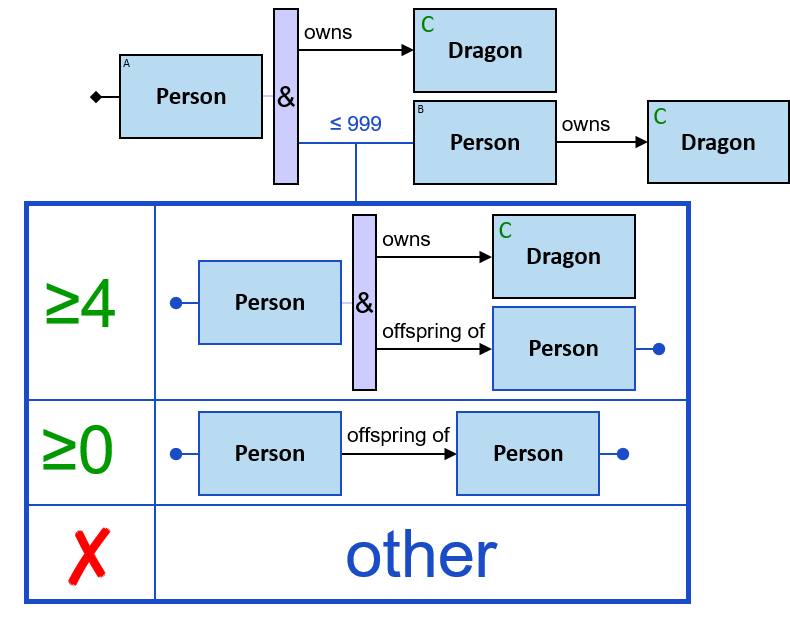
See also Q290, Q329.

Referencing Expression-Tags

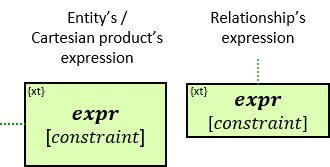
Each green rectangle has an expression-tag on its top-left corner, depicted by an index wrapped in curly brackets (‘{xt}’). An expression-tag represents the result of the evaluation of an entity’s expression, relationship’s expression, or Cartesian product’s expression - for a given assignment.

Expression-tags and aggregation-tags are jointly called EA-tags. Each EA-tag has a unique positive integer index. If an EA-tag is referenced at least once - it is depicted in bold purple. Otherwise - it is depicted in black.

Expression-tags may be referenced:

• in an entity, relationship, or Cartesian product’s expression (see Q267v2, Q308, Q349)
• in an entity, relationship, or Cartesian product’s expression constraint (see Q108, Q109)
• in a path length constraint
• in an extended aggregator per clause (see Q114v3, Q270)
• in an A3 aggregator “aggop …” clause (see Q116)
• in an extended M1/M2/M3 aggregator “[all but] 𝑘 …” clause (see Q220, Q262)
• in an M3 aggregator “with min/max …” clause (see Q130)
• in an A1/A2/A3 aggregator constraint (see Q120, Q255)

Q108: Any person who has the same birth date as Brandon Stark

{1} is a property of the only assignment to A. {2} is a property of each unique assignment to B.

For any quantifier except All:

• Any EA-tag defined in a branch, except expression-tag of an entity’s expression where the entity is left of the quantifier and the entity’s expression is right of it, can only be referenced in that branch.

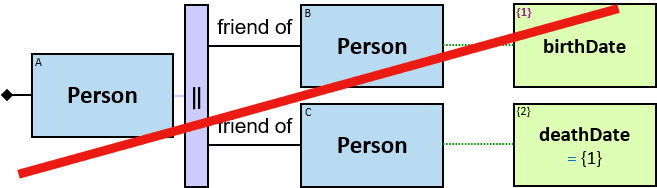
Similarly, for any horizontal quantifier except All:

• Any EA-tag defined in a branch, except expression-tag of a relationship’s expression where the relationship is above the quantifier, and the relationship’s expression is below it, can only be referenced in that branch.

For each entity/relationship/Cartesian product - if the same expression is used more than once - the same expression-tag will be assigned (see also Q267v3, Q311):

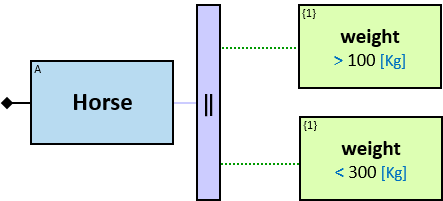
Self or circular references are invalid:

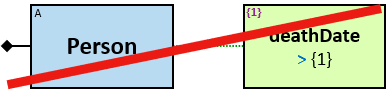
Q111: Any person A who has no friends with whom A shares a birthdate

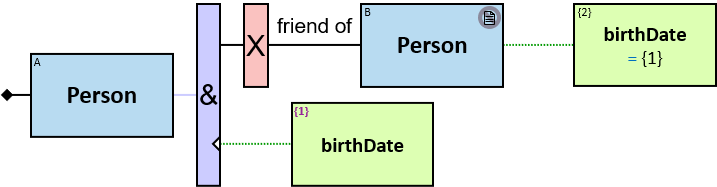
An EA-tag defined right of a negator can only be referenced right of that negator.

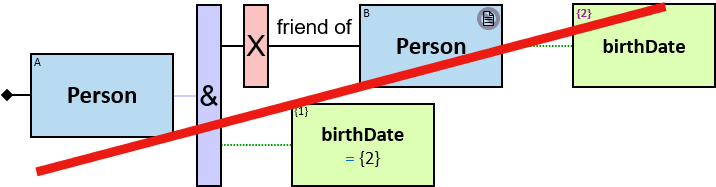
Q353: Any person A that in the day A turned two years old - at least one person was born, but there is no such person A became a friend of since A reached 20

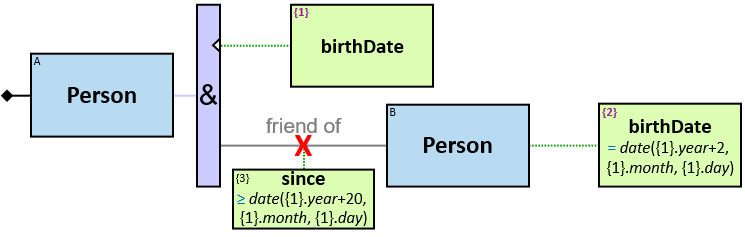
A relationship’s expression defined below a relationship-negator can only be referenced in that chain.

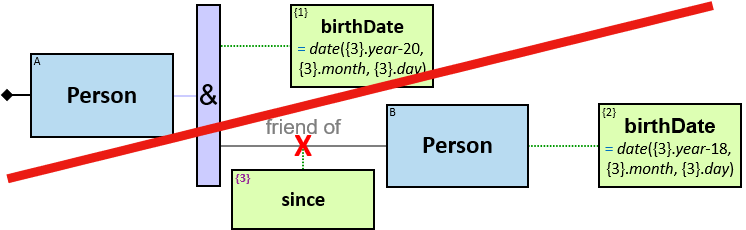
Composite properties and subproperties are tagged and can be referenced similar to ordinary properties:

Q109: Any person A whose parent owned a horse or a dragon before A’s birth (two versions)

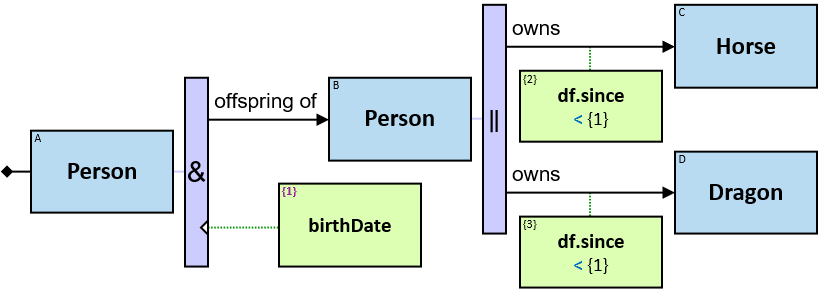
Q110: Any three dragons with cyclic freezes of more than 100 minutes, in chronological order, within six months, and their owners (if any)

Q112: Any person who owned a horse and a dragon at the same timeframes (three versions)

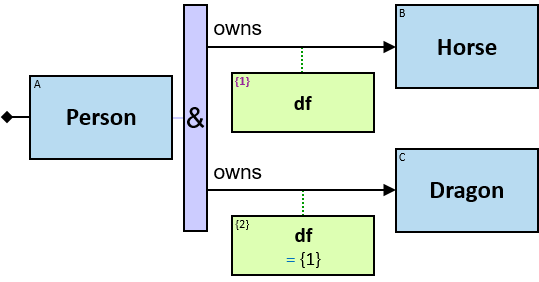
The subproperties can be compared one-by-one:

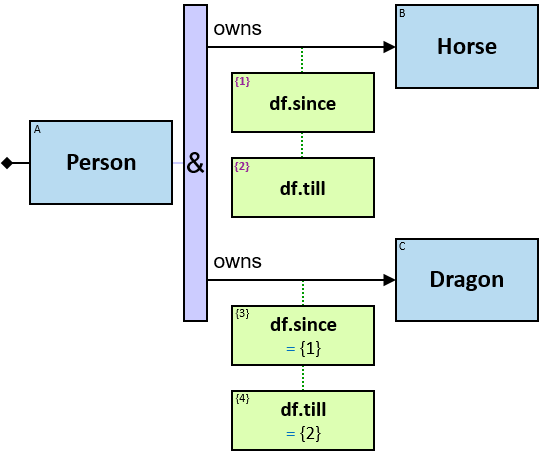
The order of the expressions along a chain does not matter. The following representation is valid, as well:

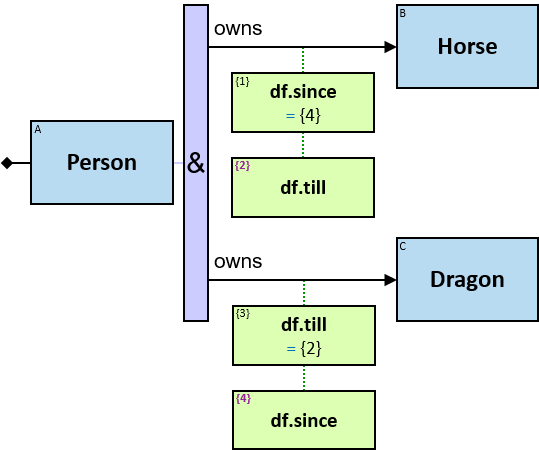
Q266: Any person A who has the same name (first and last) as A’s parent (two versions)

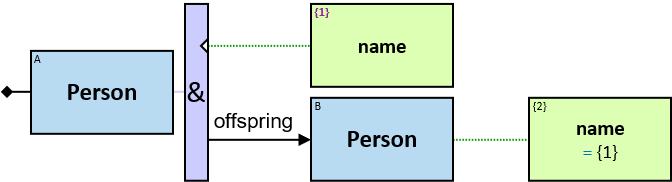
Q267: Any person who was a member of two guilds at overlapping timeframes (three versions)

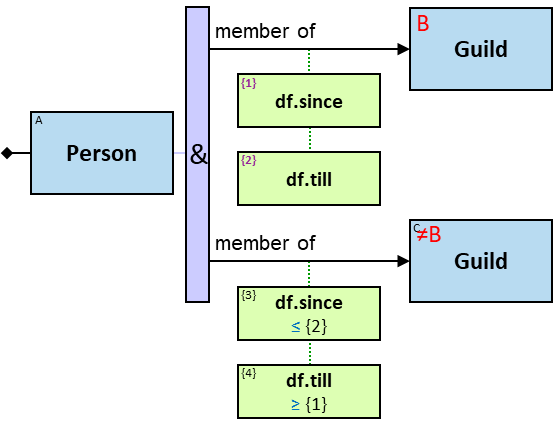
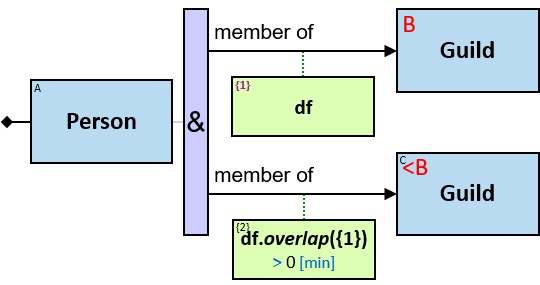
The following version also covers some cases where one membership has either a null (unknown) start date or a null (unknown) end date:

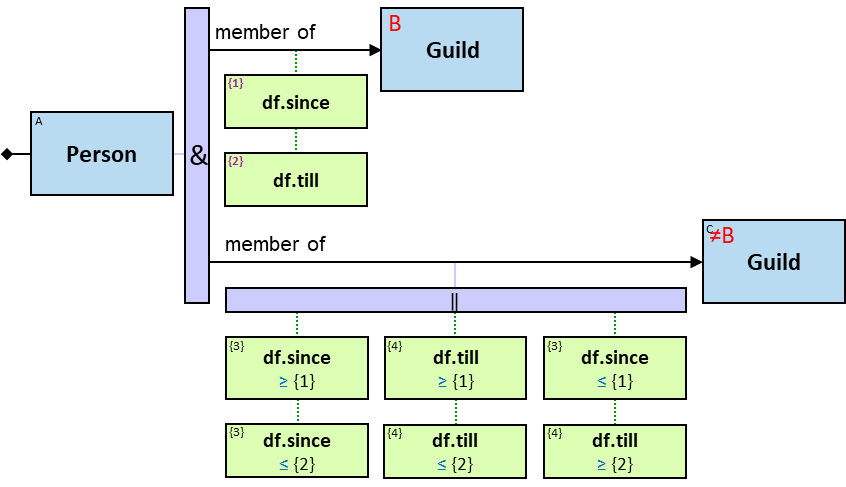
Aggregators

One can use an order constraint to represent patterns such as Any person who owns at least two horses, but it is quite cumbersome for patterns such as Any person who owns at least 20 horses. Patterns such as Any dragon that froze dragons more than ten times or Any dragon that froze dragons for a cumulative duration longer than 100 minutes cannot be expressed without aggregators.

An orange rectangle represents an aggregator. It is composed of two parts:

• The upper part (dark orange) defines how assignments are split into disjoint sets (per clause)
• The lower part (light orange) defines an aggregate expression that is evaluated per each set and may contain a constraint on the result of the evaluation of the aggregate expression

Here are three examples:

First example: Any person who owns at least 20 horses (Q59)

All assignments to the pattern, ignoring the aggregator, are found, and split into sets. In each set, all the assignments to A are identical. Only sets with more than 20 assignments to B are valid pattern assignments.

Second example: Any dragon that froze dragons more than ten times (Q71)

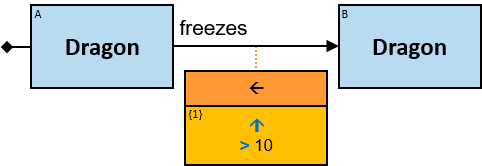
All assignments to the pattern, ignoring the aggregator, are found, and split into sets. In each set, all the assignments to A are identical. Only sets with more than ten assignments to the relationship are valid pattern assignments.

Third example: Any pair of dragons (A, B) where A froze B for a cumulative duration longer than 100 minutes (Q86)

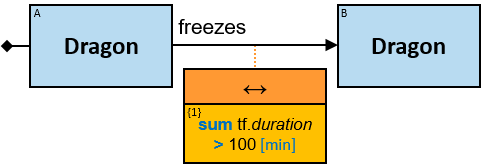
All assignments to the pattern, ignoring the aggregator, are found, and split into sets. In each set, all the assignments to both A and B are identical. Only sets where the sum of the duration of all freezes relationships is greater than 100 minutes are valid pattern assignments.

Evaluating an aggregator:

• Step 1: All assignments to the pattern excluding this aggregator and without constraints based on this aggregation-tag (‘at’) are found
  • In the first example: all (person, horse) pairs (A, B) where A owns B
  • In the second and third examples: all dragon pairs (A, B) where A froze B
• Step 2: The assignments are split into disjoint sets. In each set - the assignment to the entities listed in the per clause is identical. Each set is to be aggregated separately.
  • In the first and second examples: In each set - all assignments to A are identical
  • In the third example: In each set - all assignments to both A and B are identical
• Step 3: Per each set of assignments - at is evaluated
  • In the first example: per person A: at = number of horses A owns
  • In the second example: per dragon A: at = cumulative number of its freezes relationships to all dragons
  • In the third example: per dragon pair (A, B): at = sum of the duration of all freezes relationships from A to B
• Step 4: Per each set of assignments: the aggregation constraint (if given) and any other constraint that is based on this aggregation-tag are evaluated
  • In the first example: the aggregation constraint is at ≥ 20
  • In the second example: the aggregation constraint is at > 10
  • In the third example: the aggregation constraint is at > 100 [min]
• Step 5: Each set of assignments for which the constraint is satisfied - is a valid assignment to the pattern

Next, we will define three aggregator types: A1, A2, and A3. Steps 1, 2, 4, and 5 are identical for all types. Step 3 is different, as sets are aggregated in different ways.

Let 𝑆 denote the set of all assignments to the pattern excluding this aggregator (subject to aggregators evaluation order) (that is step 1 above).

Upper part

Let 𝑇 denote a Cartesian product of one or more entity-tags.

For all aggregator types (A1, A2, A3, M1, M2, M3, and R1), the per clause has one of the following formats:

• ‘et1 × et2 × …’:

  𝑇 = et1 × et2 × …

• ‘←’:

  𝑇 = entity-tag directly left of the aggregator

• ‘→’:

  𝑇 = entity-tag directly right of the aggregator not wrapped with a negator nor preceded by a None quantifier (valid only when there is exactly one such entity-tag (A1: see Q246)

• ‘⟷’:

  𝑇 = et1 × et2 where et1 is directly left of the aggregator, and there is a single entity directly right of the aggregator not wrapped with a negator nor preceded by a None quantifier - et2 (A2: see Q75)

Wherever possible, the notations ‘←’, ‘→’ and ‘⟷’ are used instead of entity-tags.

Next, let TA denote a of all unique assignments to 𝑇 in 𝑆. TA[n] is the n’th unique assignment to 𝑇.

Let S(n) denote a subset of 𝑆: the set of all assignments composed of TA[n] (that is step 2 above).

The upper part is optional. When there is no upper part - 𝑆 is not split.

Lower part

The lower part contains an aggregation-tag, an aggregate expression, and optionally a constraint on the result of the evaluation of the aggregate expression.

The aggregation-tag is on the top-left corner and is depicted by an index wrapped in curly brackets (‘{at}’). An aggregation-tag represents the result of the evaluation of the aggregate expression for a given set of assignments.

For each entity/relationship/Cartesian product - if the same expression/aggregation is used more than once - only one EA-tag will be assigned (see Q64, Q73v2, Q82v2).

at is evaluated per each TA[n]. In the first example above, {1} is evaluated per each unique assignment to A in 𝑆. at is a calculated property of TA[n]. When there is no upper part - at is a global property (see {1} in Q82v3, {1} in Q372, {2} in Q356).

Aggregation-tags may be referenced:

• in an entity, relationship, or Cartesian product’s expression (see Q315, Q317)
• in an entity, relationship, or Cartesian product’s expression constraint (see Q337, Q338v2)
• in a path length constraint
• in an extended aggregator per clause (see Q211)
• in an A3 aggregator “[all but] 𝑘 …” clause (see Q129)
• in an M3 aggregator “with min/max …” clause (see Q91)
• in an extended M1/M2/M3 aggregator “[all but] 𝑘 …” clause (see Q212)
• in an A1/A2/A3 aggregator constraint (see Q125, Q127, Q332v2)

A1 Aggregator

Let 𝐵 denote a list of Cartesian products of entity-tags. 𝐵 must be nonempty and must not be composed of entity-tags composing 𝑇.

The lower part of an A1 aggregator contains the following elements:

• One of the following:

  • ‘et11 × et12 × … ∪ et21 × et22 × … ∪ …’ (all products have the same arity):

    𝐵 = [et11 × et12 × … , et21 × et22 × … , …] (‘∪’ - see Q295)

  • ‘←’:

    card(𝐵) = 1; B[1] = [et] where et is directly left of the aggregator (see Q249, Q250)

  • ‘→’:

    𝐵 = [et1, et2, …] where et1, et2, … are directly right of the aggregator and not wrapped with a negator nor preceded by a None quantifier (equivalent to ‘et1 ∪ et2 ∪ …’) (see Q294, Q175, Q176 where card(B)>1)

  • ‘⟷’:

    𝐵 = [et × et1, et × et2, …] where et is directly left of the aggregator and et1, et2, … are directly right of the aggregator and not wrapped with a negator nor preceded by a None quantifier (equivalent to ‘et × et1 ∪ et × et2 ∪ …’)

  Let BA(n, o) denote the list of all assignments to B[o] in S(n)

• aggregation-tag: at(n) = |BA(n, 1) ∪ BA(n, 2) ∪ …_|

  We are using card(union(all assignments to all elements in B)) instead of sum(card(assignment to one element in B)) since two elements in 𝐵 may have the same assignment (see Q175), and we are counting distinct assignments to all elements in 𝐵 per 𝑛.

  When an optional part has no assignments, A1 aggregation-tags defined right of the ‘O’ are evaluated to zero (see Q125).

• an optional constraint on at(n)

  For each 𝑛: S(n) is reported only if at(n) satisfies the constraint

  Note that a ‘= 0’ constraint cannot be satisfied unless the entities composing B are right of an ‘O’, as such constraint means that there are no assignments to the pattern excluding this aggregator. Similarly:

  • no constraint is equivalent to ‘> 0’ constraint
  • ‘≠ expr’, ‘< expr’, and ‘≤ expr’ constraints are not satisfied when at(n) is zero
  • ‘= expr’, ‘≥ expr’, and ‘∈ [expr1, expr2]’ constraints are not satisfied when at(n) is zero even if expr is evaluated to zero

A1 location:

• Below a relationship/path

  A relationship/path with an A1 below it may have a relationship/path-negator (see Q63-Q66) and may be wrapped with an ‘O’ (see Q82v2, Q126).

• Below a quantifier-input (excluding quantifier at the start of the pattern)

  See Q305v1, Q121v1, Q122. A quantifier-input with an A1 below it may be wrapped with an ‘O’.

• Below the pattern’s start (even when followed by a quantifier)

  See Q27, Q261, Q332.

• If all entities in T ∪ B are in a sequence: if all the entities in 𝑇 appear right of all the entities in 𝐵: left of the rightmost entity in 𝑇 (see Q247). Otherwise: right of the leftmost entity in 𝑇 (see Q243)
• If entities in T ∪ B are in different branches of a quantifier: below the quantifier-input (see Q27)

Q59: Any person who owns at least 20 horses

{1} is a property of each unique assignment to A in 𝑆.

Q60: Any dragon that was frozen by exactly five dragons

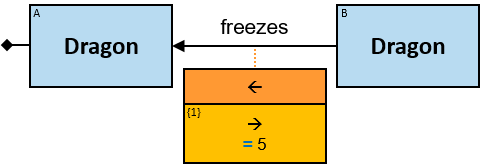
If some dragon B froze some dragon A more than once - B would still be counted only once per A. A1 counts distinct entity assignments.

Q61: Any entity that owns more than two entities

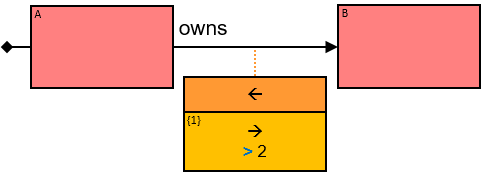
Q62: Any person who has paths of length up to four to more than five people

Q136: Any dragon A that froze (dragons that froze dragons B). The cumulative number of distinct Bs (per A) is greater than 100 (two versions)

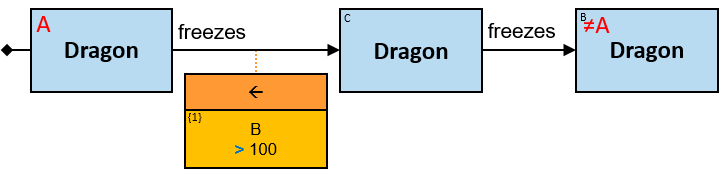
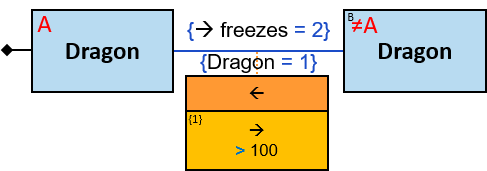
Q177: Any dragon A frozen by at least ten dragons and froze each of those (two versions)

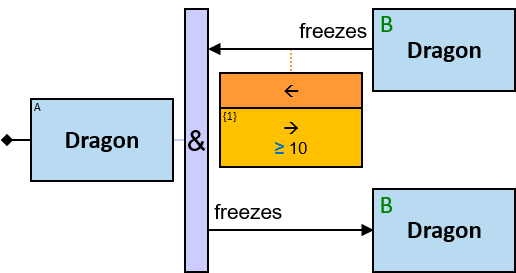
First, any pair (A, B) matching the pattern excluding the aggregator is found. Then, the aggregation constraint is checked: For each assignment to A, there are at least ten assignments to B.

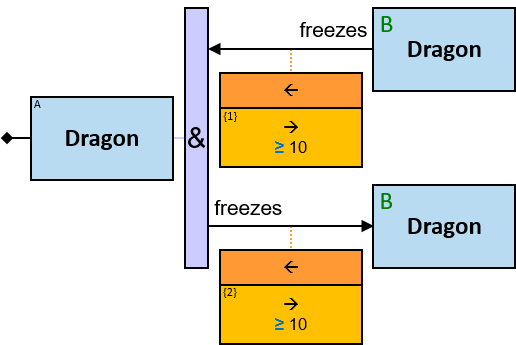
First, any pair matching the pattern excluding the aggregators is found. Then, the aggregation constraints are checked one by one:

For each assignment to A:

• There are at least ten assignments to B such that B froze A
• There are at least ten assignments to B such that A froze B

Q178: Any dragon A either (i) frozen by exactly ten dragon and froze at least one dragon which is not one of those, (ii) frozen by exactly ten dragon and froze at least two of those, or (iii) frozen by more than ten dragons and froze at least one dragon

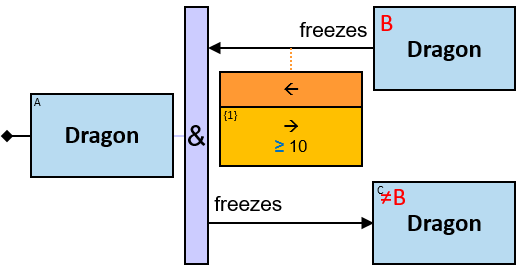
First, any dragon triplet (A, B, C) matching the pattern excluding the aggregator is found. Then, the aggregation constraint is checked:

For each assignment to A, there are at least ten assignments to B such that (B froze A, and A froze a dragon that is not B)

Q85: Any dragon that froze at least ten dragons and was frozen by at least ten dragons (two versions)

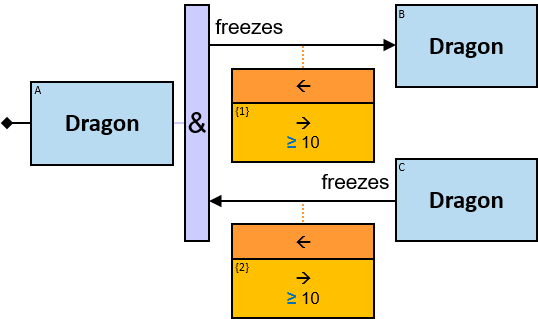
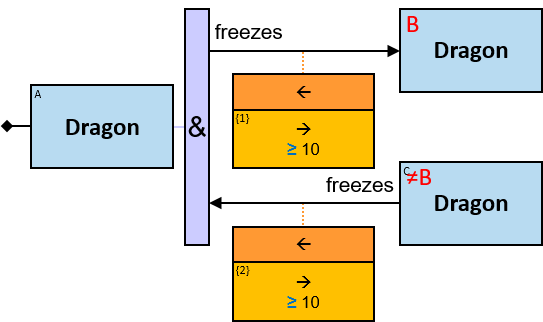
First, any dragon triplet (A, B, C) matching the pattern excluding the aggregators is found. Then, the aggregation constraints are checked one by one:

For each assignment to A:

• There are at least ten assignments to B such that A froze B, and a dragon other than B froze A
• There are at least ten assignments to C such that C froze A, and A froze a dragon other than C

Hence, for each assignment to A:

• A froze at least ten dragons, and either (i) only one dragon froze A - which is not one of those, or (ii) at least two dragons froze A
• At least ten dragons froze A, and either (i) A froze only one dragon - which is not one of those, or (ii) A froze at least two dragons

Hence, A froze at least ten dragons, and at least ten dragons froze A

Q101: Any person who owns at least five white horses

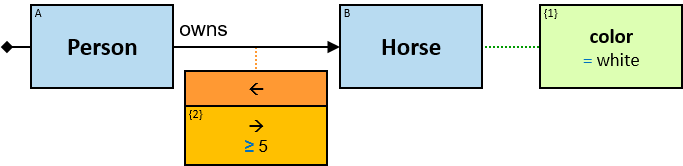
Q102: Any dragon A that was frozen by exactly two dragons, each of which was frozen at least once. A might have been frozen by additional dragons that were never frozen

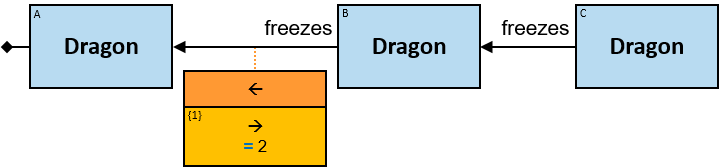
Q166: Any dragon that more than five Sarnorians own a dragon that froze it

Q246: Any dragon B that froze at least one dragon and was frozen by more than ten dragons

{1} is a property of each unique assignment to B in 𝑆.

Q247: Any dragon C that more than ten dragons froze dragons that froze it

Q113: Any person A who has at least five friends with whom A shares a birthdate

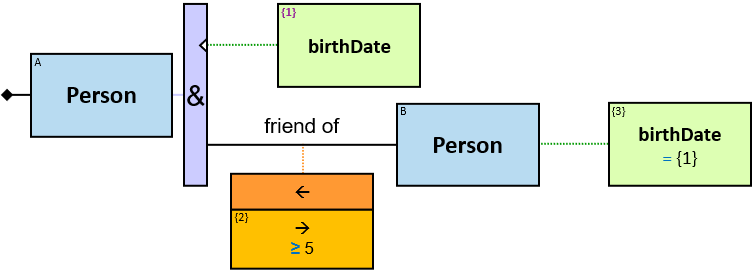
Q114: Any person who owns at least five horses of the same color (versions 1, 2)

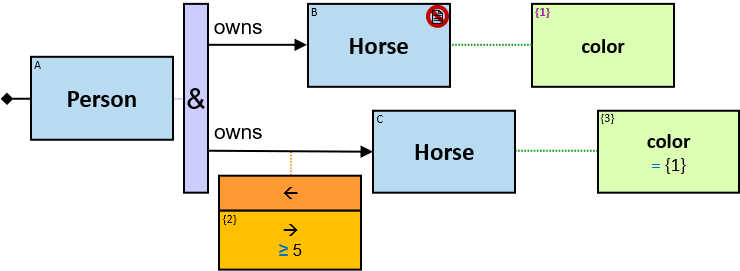
B is explicit latent to avoid redundant results. Were B not latent, each pattern assignment would have one of A’s dragons assigned to B and all A’s dragons of the same color assigned to C. When B is latent, all such reported results are identical, hence, reported only once.

The following pattern avoids redundant results as well:

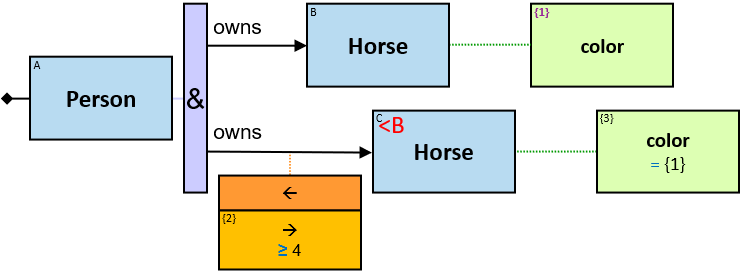
Q218: Any person who owns at least five entities of the same type (version 1)

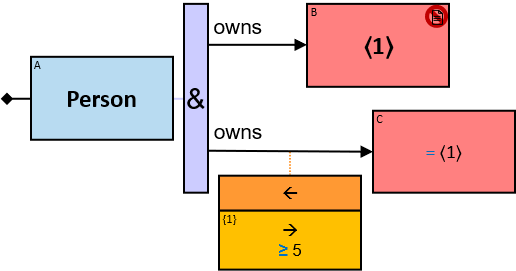
Q292: Any person A that at least 80% of A’s horses are black

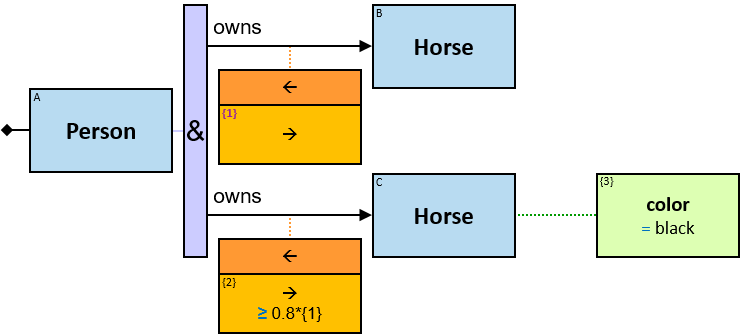
Q63: Any Masons Guild member who more than fifty Masons Guild members are not friends of

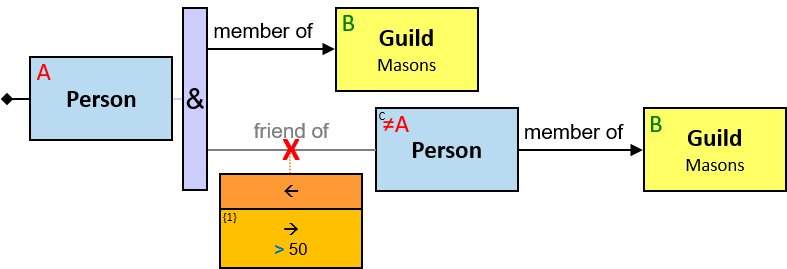
Q65: Any person A who does not own more than two things that (at least) one of A’s parents owns/owned

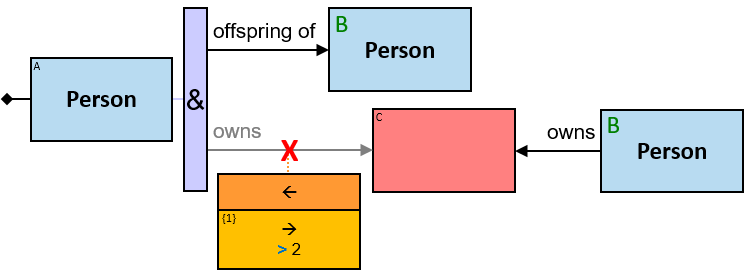
Q66: Any person from whom more than five people do not have a path of length up to six

Q151: Any horse owned by more than ten people, at least one is Sarnorian. Only the Sarnorian owners should be reported

Q152: Any horse owned by more than ten people. Only the Sarnorian owners should be reported

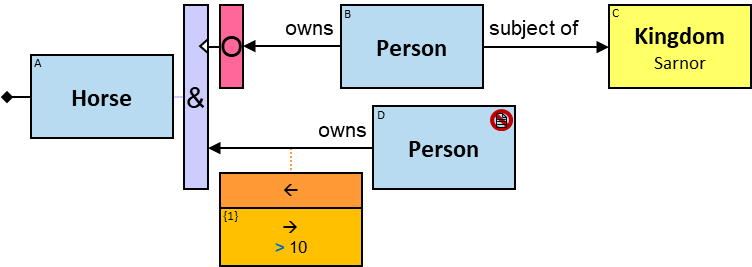
Q125: Any dragon that the number of dragons it froze is greater than the number of dragons that froze it

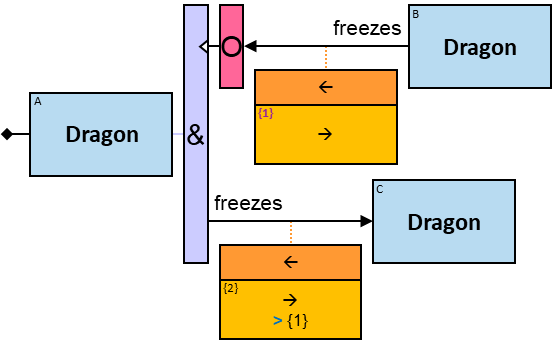
{1} is evaluated to zero when the optional part has no valid assignments.

Q126: Any dragon that the number of dragons it froze is greater than the number of dragons it did not freeze

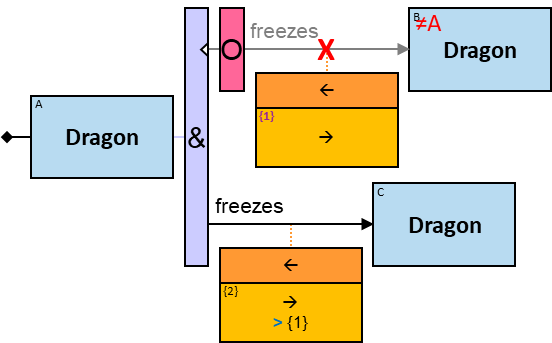
Q249: Any triplet of sets (people A, dragons B, horses C) where (i) any person in A owns at least one dragon in B and at least one horse in C, (ii) any dragon in B is owned by at least ten people in A, and (iii) any horse in C is owned by at least ten people in A

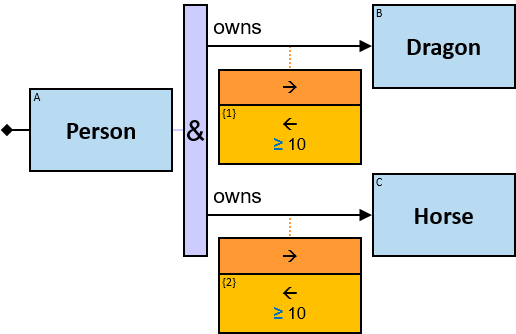
Q250: Any triplet of sets (people A, dragons B, horses C) where (i) any person in A owns at least one dragon in B or at least one horse in C, (ii) any dragon in B is owned by at least ten people in A, and (iii) any horse in C is owned by at least ten people in A

Q344: Any triplet of sets (people A, dragons B, horses C) where (i) any person in A owns at least one dragon in B and at least one horse in C, (ii) any dragon in B is owned by at least ten people in A, and (iii) any horse in C is owned by less than five people in A

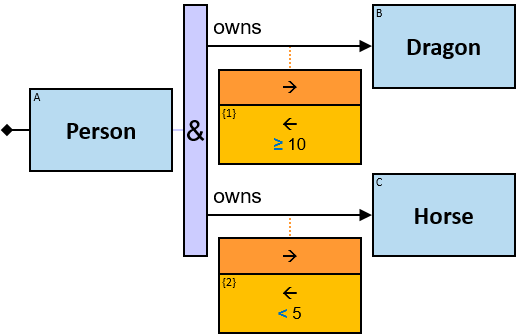
Q345: Any triplet of sets (people A, dragons B, horses C) where (i) any person in A owns at least one dragon in B and does not own at least one horse in C (ii) any dragon in B is owned by at least ten people in A, and (iii) any horse in C is not owned by at least ten people in A

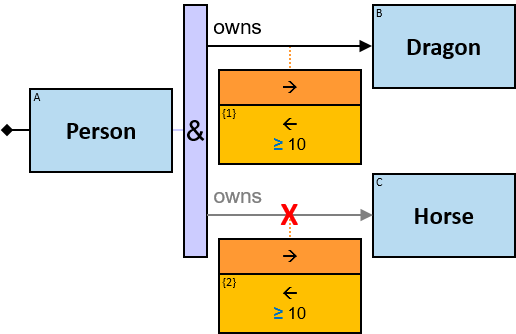
Q82: Any dragon that froze all other dragons. Alternative phrasing: Any dragon for which there is no dragon (besides itself) it did not freeze (version 2)

The dragons that were frozen will not be a part of the assignment.

Q360: Any dragon that (froze or fired at) all other dragons. Alternative phrasing: Any dragon for which there is no dragon (besides itself) it did not (freeze or fire at) (version 2)

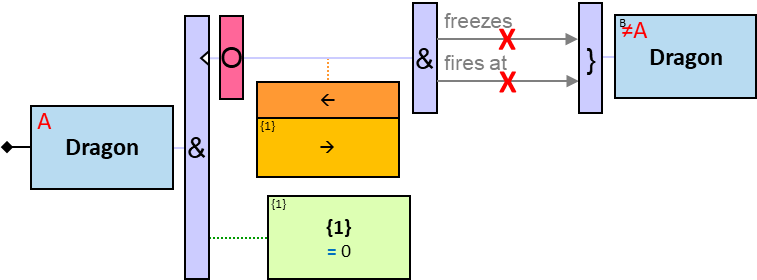
Q64: Any dragon that no more than four dragons owned by Sarnorians did not freeze it

Q165: Any dragon that no more than four Sarnorians own a dragon that did not freeze it

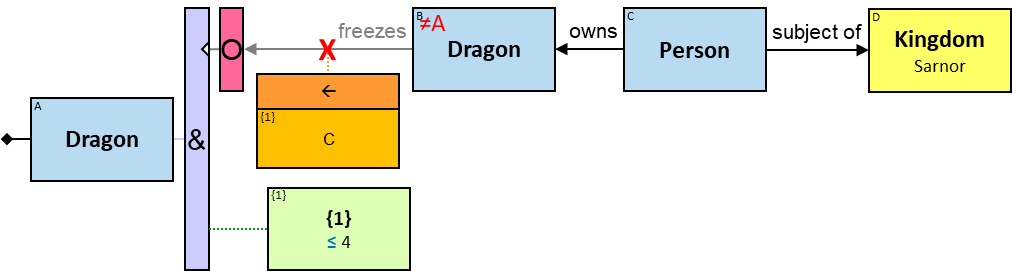
Q206: Any dragon A that for each of no more than four Sarnorians C there is a dragon C does not own that did not freeze A

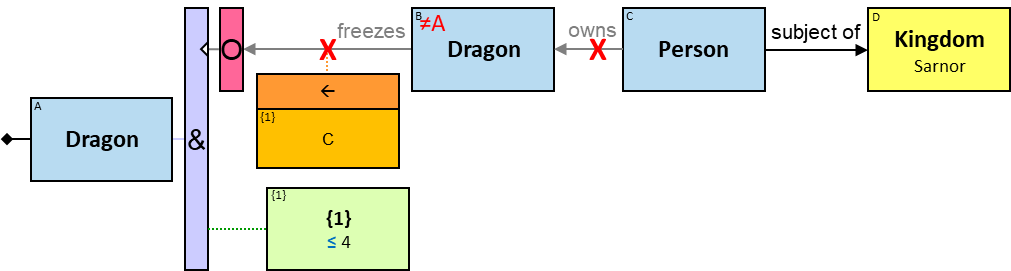
Q305: Any person A that the number of horses A owns plus the number of dragons A owns - is at least ten (two versions)

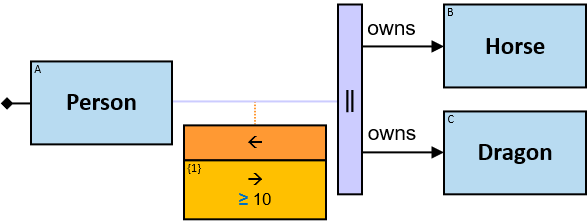
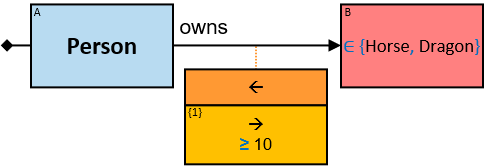
Q121: Any dragon that froze or fired at at least ten dragons (two versions)

‘→’ is the entity directly right of the combiner.

Note that any dragon that was both frozen and fired at - would be counted only once.

Q122: Any dragon that fired at dragon B and fired at a dragon that fired at B - for at least ten different B’s

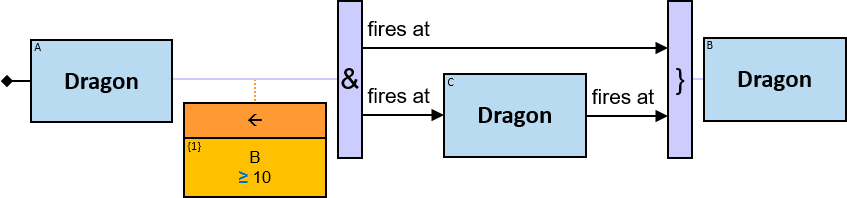
Q294: Any dragon that fired at Balerion and at least nine other dragons

Q175: Any dragon that froze some dragon at least once and fired at some dragon at least once. The number of dragons it froze/fired at – is at least ten

Note that if a dragon were both froze and fired at - it would be counted only once. A1 counts distinct entity assignments.

Q298: Any dragon A where (i) there is at least one black dragon A froze (ii) there is at least one white dragon A did not freeze, (iii) there is no gold dragon A froze, (iv) there is no silver dragon A did not freeze, and (v) the number of black or red dragons A froze plus the number of white and blue dragons A did not freeze - is at least ten. Report all black and red dragons that A froze and all white and blue dragons that A did not freeze

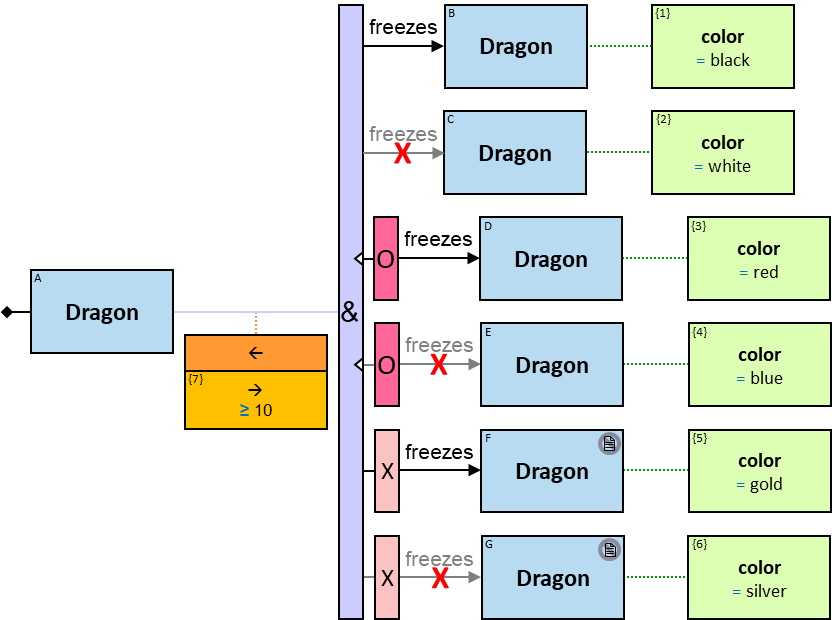
Note that the entities that are right of a negator are not aggregated, but the entities that a right of a relationship/path-negator and no negator are aggregated. Compare with Q358.

Q176: Any dragon that either (i) froze at least one dragon and fired at at least one dragon it did not freeze. The number of dragons it froze/fired at is at least ten, or (ii) froze at least ten dragons

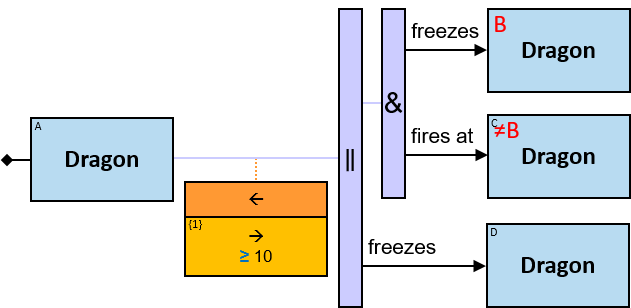
Q293: Any person A that at least 80% of the horses owned by A and/or by (at least) one of A’s parents - are jointly owned by A and by (at least) one of A’s parents

Q288: Any person A who owns a dragon that froze more dragons than any dragon owned by any of A’s ancestors

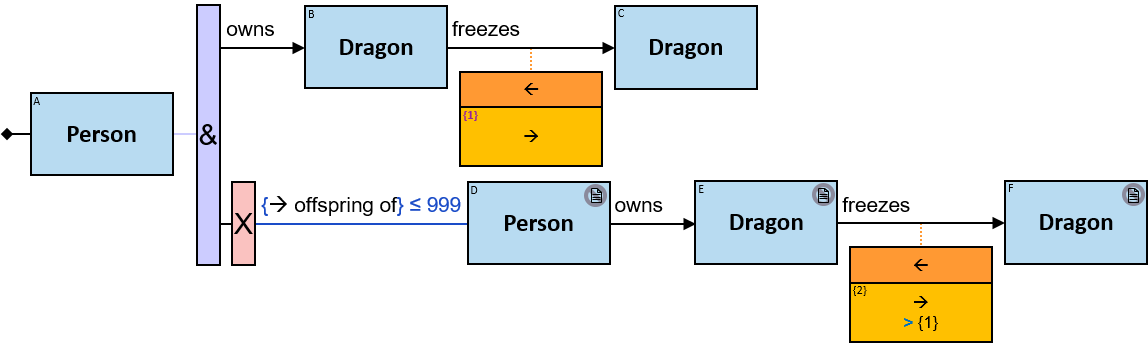
Q290: Any path of length up to ten between Rogar Bolton and Robin Arryn that does not contain hubs (in this pattern - hubs are entities with degree ≥ 1000)

Q329: Any Sarnorian who has paths of length up to six to more than five Omberians, Each of these paths passes through Rogar Bolton

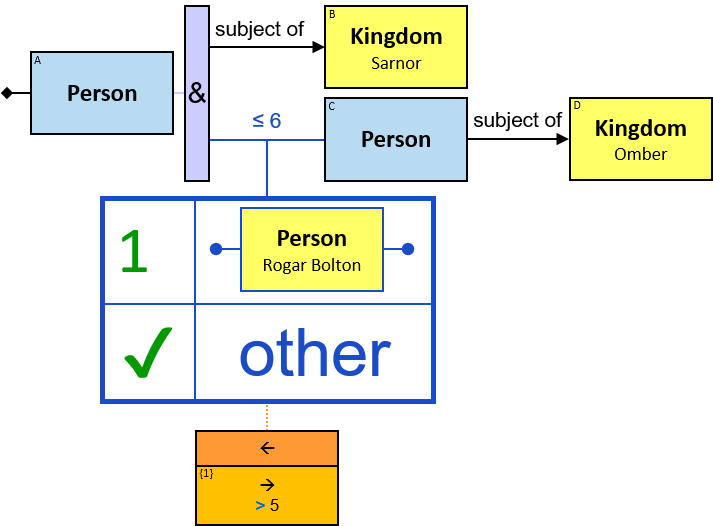
Q295: Any person A that the number of dragons A owns plus the number of dragons A does not own that A’s dragons fired at - is at least ten

Note that if any of A’s dragons were fired at one of A’s other dragons - it would not be counted twice.

Q248: Any pair of dragons (A, C) where A froze more than ten dragons that froze C

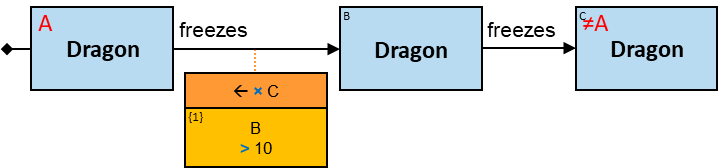
{1} is a property of each unique assignment to A × C in 𝑆.

Q243: Any pair of people (A, D) where at least five of A’s dragons froze one or more D’s dragons

Q244: Any pair of people (A, D) where at least five of A’s dragons froze D’s dragons, and at least five D’s dragons were frozen by one or more A’s dragons

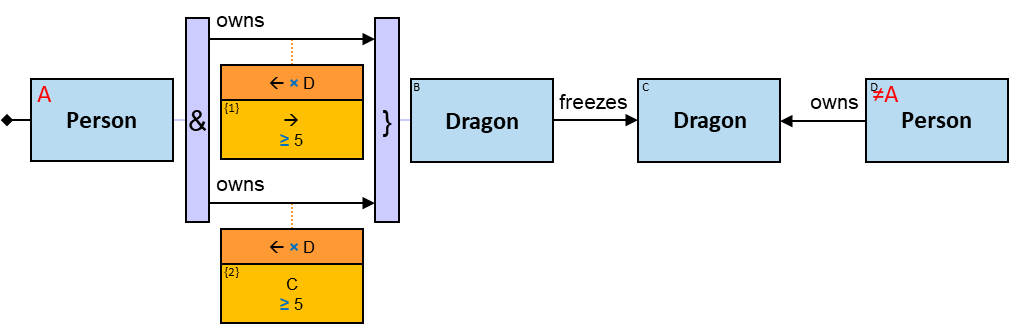
Q27: Any person A where there are less than 500 horses (combined) of the same colors as A’s owned horses

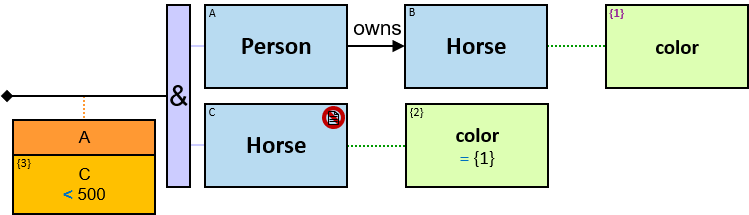
Q28: Any person who owns a horse of a rare color (there are less than 500 horses of that color)

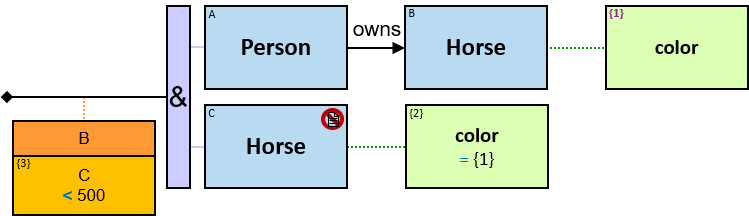
Patterns Q346, Q352, and Q355, are similar in structure, but the aggregation is different:

Q346: Any dragon that froze at least ten dragons of the colors of horses of its owners

Q352: Any dragon that froze at least ten dragons of the colors of horses of one of its owners

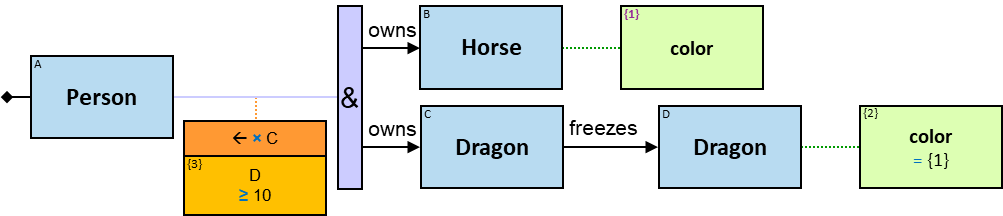
Q355: Any dragon that froze at least ten dragons of the color of one horse of one of its owners

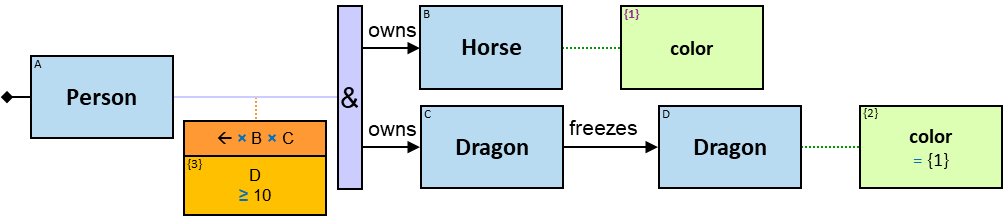
Q335: Any person and that person’s parent for whom there is no horse that both are its owners

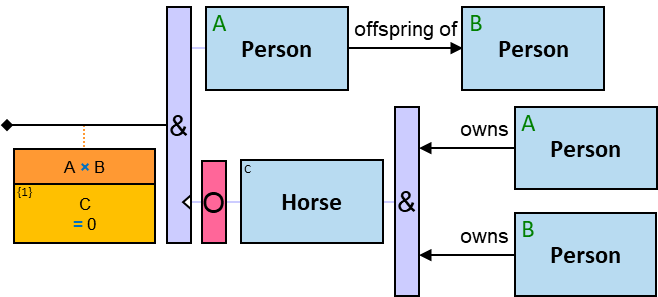
Q334: Any dragon A for which there is no dragon B that A both froze and fired at

Q207: Any pair of dragons where the difference between the number of dragons that one of them froze and the number of dragons that the other froze is less than 10

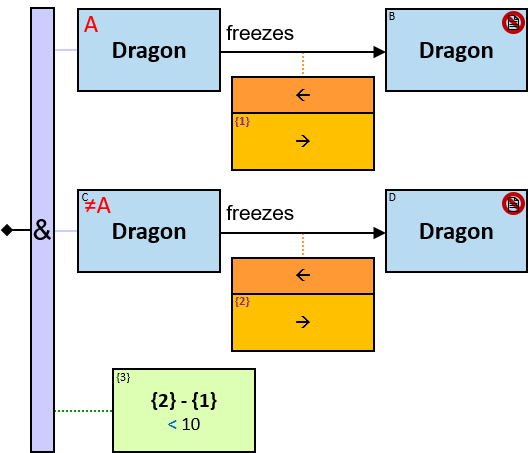
{3} is a property of each unique assignment to A × C in 𝑆.

Q279: Any pair of people (A, E), each own dragons, where no A’s dragon froze any of E’s dragons

Q82: Any dragon that froze all other dragons. Alternative phrasing: Any dragon for which there is no dragon (besides itself) it did not freeze (version 3)

{1} is a global property.

In contrast to Q82v1 and Q82v2, the frozen dragons will be a part of the assignment.

Q360: Any dragon that (froze or fired at) all other dragons. Alternative phrasing: Any dragon for which there is no dragon (besides itself) it did not (freeze or fire at) (version 3)

Q375: The difference between the number of white dragons and the number of black dragons

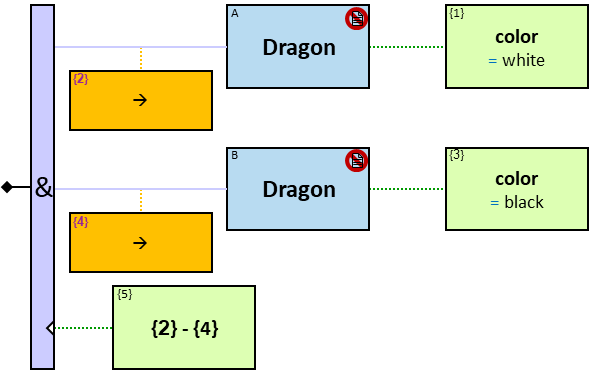
{2}, {4} and {5} are global properties. {5} is a global expression.

A2 Aggregator

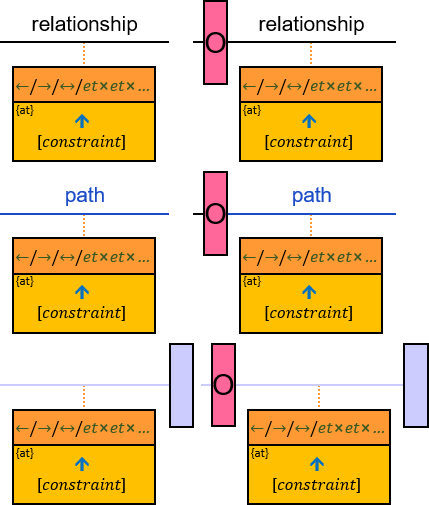
Let 𝑅 denote a list where each element is a pattern-relationship/pattern-path. 𝑅 must be nonempty.

The lower part of an A2 aggregator contains the following elements:

• ‘↑’ (an arrow pointing to the relationship/path on top of the aggregator):

  When A2 appears below a relationship/path - card(𝑅) = 1; R[1] = the relationship/path.

  When A2 appears below a quantifier-input - each element in 𝑅 is the relationship/path that follows one branch of the quantifier, excluding relationships/paths wrapped with a negator or a relationship/path-negator (see Q123, Q358).

  Let RA(n, o) denote the list of all assignments to R[o] in S(n).

• aggregation-tag: at(n) = |RA(n, 1) ∪ RA(n, 2) ∪ … |

  We are using card(union(all assignments to all elements in R)) instead of sum(card(assignment to one element in R)) since two elements in 𝑅 may have the same assignment (see Q100), and we are counting distinct assignments to all elements in 𝑅 per 𝑛.

  When an optional part has no assignments, A2 aggregation-tags defined right of the ‘O’ are evaluated to zero (see Q347).

• an optional constraint on at(n)

  For each 𝑛: S(n) is reported only if at(n) satisfies the constraint

  Note that a ‘= 0’ constraint cannot be satisfied, as such constraint means that there are no assignments to the pattern excluding this aggregator. Similarly:

  • no constraint is equivalent to ‘> 0’ constraint
  • ‘≠ expr’, ‘< expr’, and ‘≤ expr’ constraints are not satisfied when at(n) is zero
  • ‘= expr’, ‘≥ expr’, and ‘∈ [expr1, expr2]’ constraints are not satisfied when at(n) is zero even if expr is evaluated to zero

A2 location:

• Below the relationship/path whose assignments are counted.

  A relationship/path with an A2 below it may be wrapped with an ‘O’.

• Below the quantifier-input (except a None quantifier) that assignments to relationships/paths on its right are counted (see Q297, Q174).

  A quantifier-input with an A2 below it:

  • may be wrapped with an ‘O’ (except at the pattern’s start)
  • at least one branch of the quantifier (or subbranch of a sequence of quantifiers) must start with a relationship/path with no relationship/path-negator that is not wrapped with a negator, nor preceded by a None quantifier

Q71: Any dragon A that froze dragons more than ten times

Q72: Any dragon A that was frozen exactly ten times (two versions)

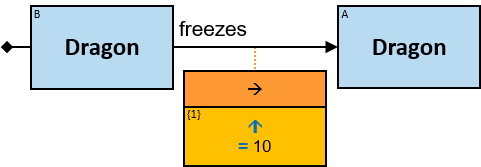
Q73: Any dragon that did not freeze dragons or froze dragons no more than ten times (two versions)

Q123: Any dragon that either froze or fired at dragons - at least ten times

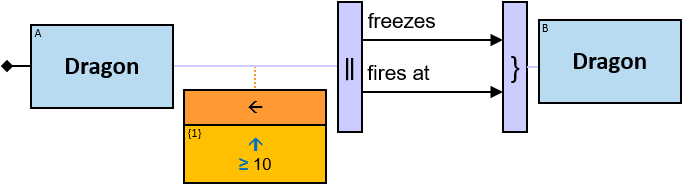
(Per assignment to A - counting the number of assignments to the relationship directly right of the quantifier)

Q104: Any person who owned white horses at least ten times (same or different horses)

Q296: Any person who owned horses at least ten times - each horse is either white or weighs more than 100 Kg (two versions)

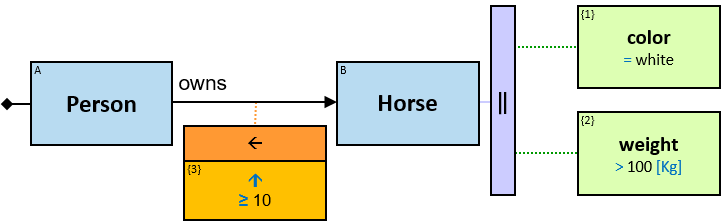
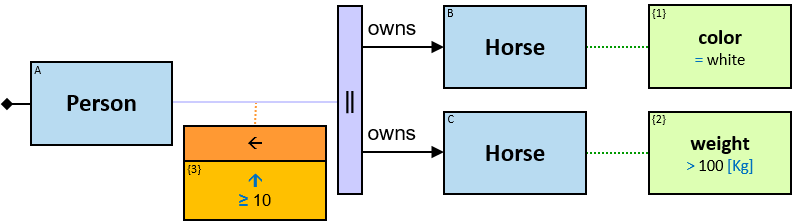
If B and C are assigned with the same graph-entity (a white horse that weighs more than 100 Kg), identical assignments to the two owns relationships would be counted only once. A2 counts distinct relationship/path assignments.

Q79: Any person with more than five paths of length up to four to other people

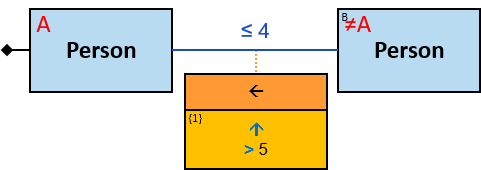
Q105: Any dragon A that was frozen exactly two times by dragons, each of which was frozen at least once. A might have been frozen by additional dragons that were never frozen

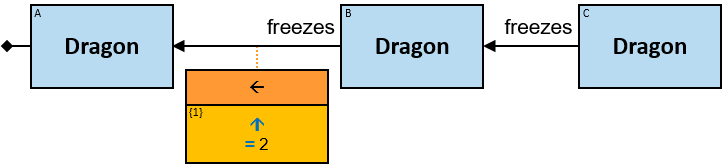
Q245: Any dragon B that was frozen at least once and froze dragons exactly twice

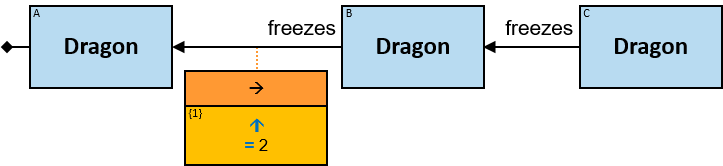
Q185: Any dragon Balerion froze at least once on or after January 1, 1010, at least once for less than ten minutes, and at least twice (on or after January 1, 1010, or for less than ten minutes)

(counting the number of distinct freezes relationships)

Q127: Any dragon that froze dragons owned by Sarnorians more times than dragons owned by Omberians

Q339: Any dragon Balerion froze more than ten times; report only those freezes that are in or after 1010

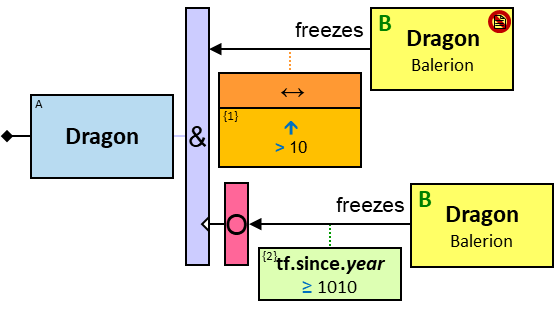
Q297: Any dragon that the number of times it fired at dragons plus the number of paths of length up to three between it and some horse - is at least ten

Q124: Any dragon that either (froze a dragon) or (fired at a dragon that fired at a dragon) - at least ten times

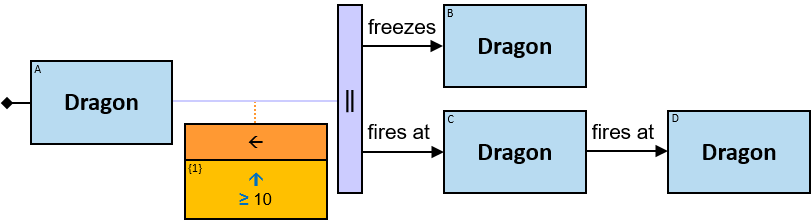
Q173: Any dragon that fired at at least two dragons and fired at least ten times

(counting the number of distinct fired at relationships). C is explicit latent to avoid redundant results (any dragon fired at would be assigned at least once to B and at least once to C).

Q174: Any dragon that either (i) froze at least one dragon and fired at at least one dragon it did not freeze, or (ii) froze at least two dragons. If (i): the number of times it froze/fired at dragons is at least ten; otherwise: the number of times it froze dragons is at least ten

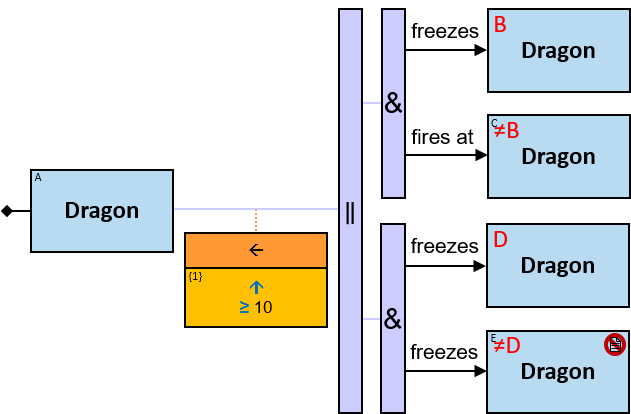
Q75: Any pair of dragons (A, B) where B froze A between eight and ten times

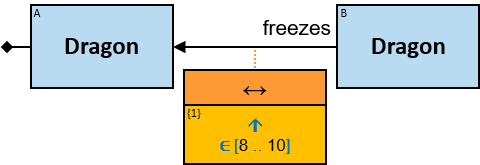
Q76: Any dragon that froze Balerion between eight and ten times

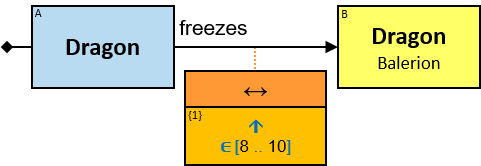
Q242: Any pair of people (A, D) where at least five times one of A’s dragons froze one of D’s dragons

Q358: Any dragon A where (i) there is at least one black dragon A froze (ii) there is at least one white dragon A did not freeze, (iii) there is no gold dragon A froze, (iv) there is no silver dragon A did not freeze, and (v) the number of times A froze black and red dragons is at least ten. Report all black and red dragons that A froze

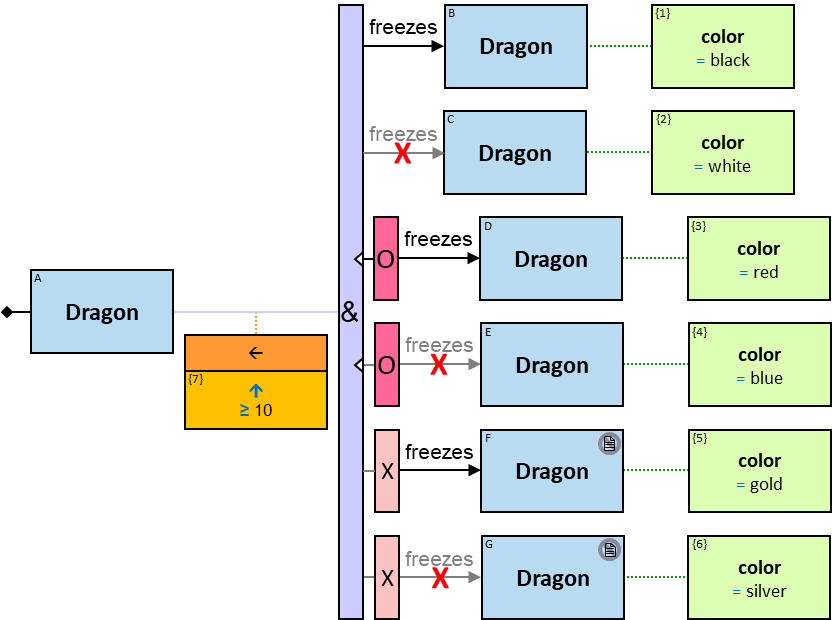
Pattern-relationships that are wrapped with a negator and pattern relationships with a relationship/path-negator are not aggregated. Compare with Q298.

Q372: The number of times dragons were frozen

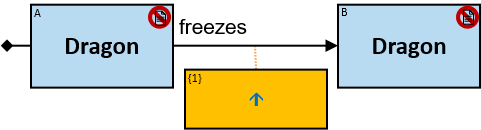
{1} is a global property.

A3 Aggregator

The lower part of an A3 aggregator contains the following elements:

• One of the following:

  • aggop expr

    aggop is min/max/avg/sum - for aggregating values of a supported type, union/intersection - for aggregating sets/bags of any type, or distinct/set/bag - for aggregating values of any type. distinct returns the number of distinct non-null evaluation results; set returns a set of all non-null evaluation results (see Q332v2); bag returns a bag of all non-null evaluation results (see Q315).

    expr is an expression composed of constants, properties, and subproperties of 𝑅 (when A3 appears below a relationship 𝑅 with no relationship-negator) (see Q86, Q354), EA-tags defined on top of the aggregator (see Q277), and EA-tags defined right of the aggregator (see Q116, Q137, Q169)

  • distinct ⟨ ett ⟩

    ⟨ ett ⟩ is an entity type-tag defined right of the aggregator (see Q167v2)

  • distinct ⟪ rtt ⟫

    ⟪ rtt ⟫ is a relationship type-tag defined on top of the aggregator or right of the aggregator (see Q366v2)

  Let BA(n) denote the list of the evaluation results of expr/⟨ ett ⟩/⟪ rtt ⟫ for all assignments in S(n).

• aggregation-tag:
  • if aggop is min/max/avg/sum/distinct/union/intersection: at(n) = aggop(BA(n)[1], BA(n)[2], …)
  • if aggop is set: at(n) = {BA(n)[1], BA(n)[2], …} (with no duplicate values and no null values)
  • if aggop is bag: at(n) = [BA(n)[1], BA(n)[2], …] (with duplicate values and no null values)

  When an optional part has no assignments, A3 aggregation-tags defined right of the ‘O’ are evaluated to null when aggop is min/max/avg, evaluated to zero when aggop is sum/distinct, and evaluated to {} / [] when aggop is set/bag/union/intersection.

• an optional constraint on at(n)

  For each 𝑛: S(n) is reported only if at(n) satisfies the constraint

  When aggop is distinct: a ‘= 0’ constraint cannot be satisfied unless ett / rtt is right of an ‘O’, as such constraint means that there are no assignments to the pattern excluding this aggregator. Similarly:

  • no constraint is equivalent to ‘> 0’ constraint
  • ‘≠ expr’, ‘< expr’, and ‘≤ expr’ constraints are not satisfied when at(n) is zero
  • ‘= expr’, ‘≥ expr’, and ‘∈ [expr1, expr2]’ constraints are not satisfied when at(n) is zero even if expr is evaluated to zero

A3 location:

• Below a relationship/path

  When A3 appears below a relationship 𝑅 and expr is composed of at least one property or subproperty of 𝑅 - 𝑅 may be wrapped with an ‘O’. Otherwise - a relationship/path with an A3 below it may have a relationship/path-negator and may be wrapped with an ‘O’.

• Below a quantifier-input (excluding quantifier at the start of the pattern)

  A quantifier-input with an A3 below it may be wrapped with an ‘O’.

• Below the pattern’s start (even when followed by a quantifier)

  See Q263.

• If all entities in 𝑇 are in a sequence: A3 appears directly right of the leftmost member of 𝑇
• If entities in 𝑇 are in different branches of a quantifier: A3 appears directly left of the quantifier

When units of measure are defined for the expression (based on the aggregation operator, on the units of measures of the properties, and on the operators that compose the expression) - they are depicted as well (see Q86, Q117).

Q86: Any pair of dragons (A, B) where A froze B for a cumulative duration longer than 100 minutes

Q87: Any dragon that was frozen at least once, and the cumulative duration it was frozen is less than 100 minutes

Q89: Any dragon that froze dragons for more than three different durations

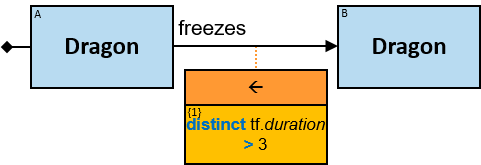
Q167: Any person whose owned entities are all of the same type (version 2)

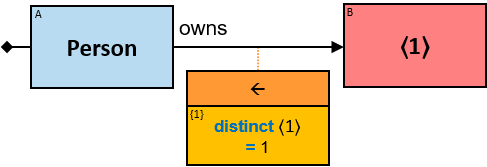
Q366: Any pair of dragons that have relationships of at least three types (version 2)

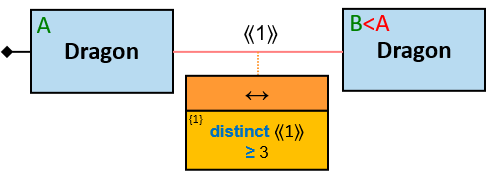
Q117: Any person whose owned horses’ average weight is greater than 450 Kg

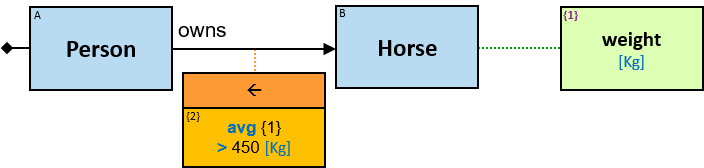
If a horse were owned twice - it would be counted only once.

Q116: Any person A that the number of distinct colors of A’s owned horses - is between one and three

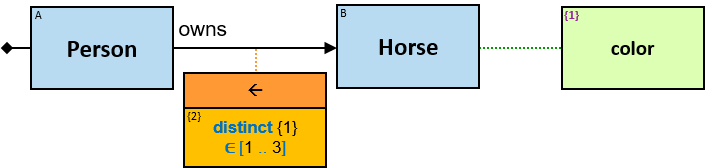
distinct does not aggregate null evaluation results. If all dragons have a null color, {2} would be equal to zero.

Q134: Any person A that the number of distinct colors of all horses owned by A’s friends - is between one and three

Q229: Any person A that the number of distinct colors of all horses owned by A’s friends and parents - is between one and three

Q135: Any person A that the average weight of all horses owned by A’s friends - is greater than 450 Kg

Note that if some person A1 is a friend of two people who jointly own a horse, this horse’s weight would be counted once.

Q137: Any dragon A that froze dragons B. Each B froze at least one dragon, which is not A. All these B’s together froze dragons for more than 100 minutes cumulatively

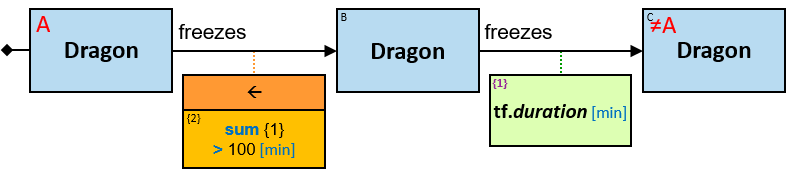
Q336: For each dragon: each time it froze some dragon for a duration longer than the average duration of all its freezes

First, any triplet (A, B, C) matching the pattern excluding the aggregator and the constraint in {2} is found. Then, {1} is evaluated per assignment to A, and then the constraint in {2} is evaluated per relationship assignment. See also Q337.

Note that a dragon that always froze dragons for the same duration is not a valid assignment to A.

Q354: Any dragon that froze one dragon and fired at another dragon, or froze a dragon and fired at more than one dragon, or fired at a dragon and froze more than one dragon, and there is some dragon that the earliest time it fired at it is earlier than the earliest time if froze any other dragon

Q139: Any person A who owns horses of the same number of colors as the number of colors of the horses owned by A’s parents cumulatively

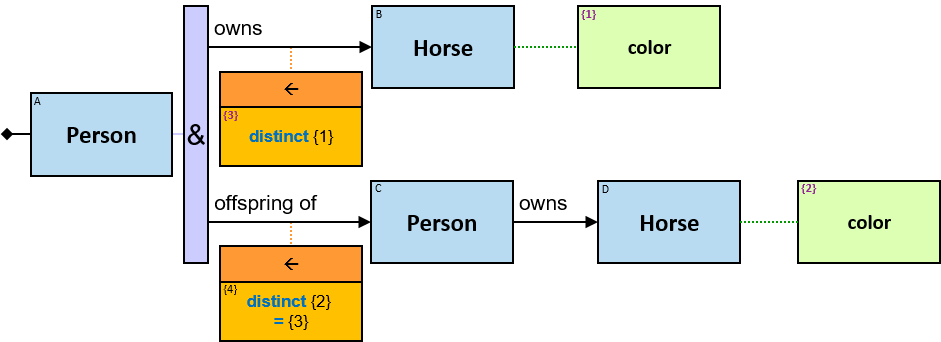
Q98: Any pair of dragons (A, X) where A froze more than three dragons and (A froze X more than ten times or for a cumulative duration of more than 100 minutes)

Q88: Any pair of dragons (A, B) where the cumulative duration A froze B is equal to the cumulative duration B froze A

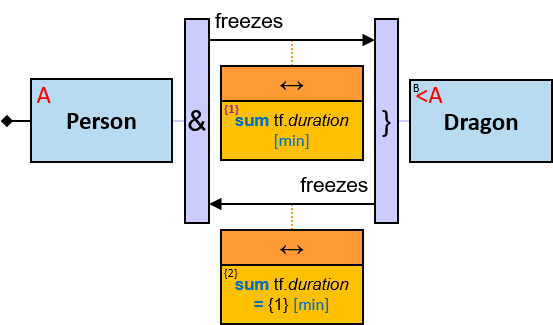
A property of entity et cannot be aggregated per et, nor per a superset of et.

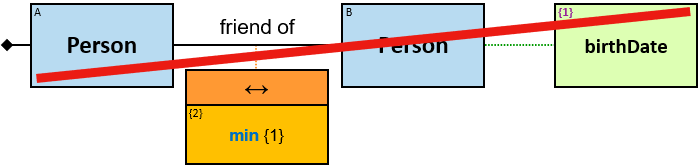
{1} is a property of B and hence cannot be aggregated per A × B.

If entity et has a property that references

• an aggregation of a property of a Cartesian product composed of et1, or
• an aggregation of a property of a relationship between et and et1

then

• a property of et cannot be constrained based on a property of et1
• a property of et1 cannot be constrained based on a property of et

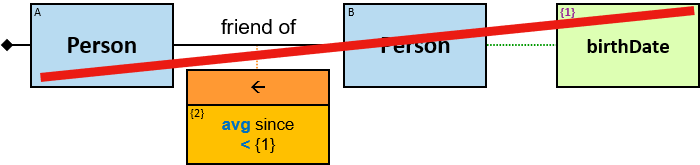
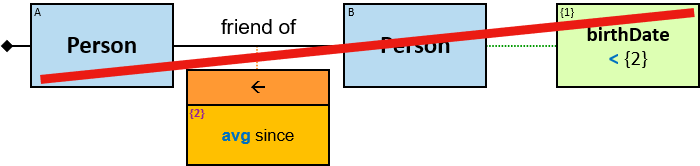
In the two patterns above, {2} - a property of A, is referencing an aggregation of a property of a relationship between A and B. Therefore, a property of A cannot be constrained by a property of B. Similarly, a property of B cannot be constrained by a property of A.

In the two patterns above, {2} - a property of B, is referencing an aggregation of a property of a relationship between A and B. Therefore, a property of B cannot be constrained by a property of A. Similarly, a property of A cannot be constrained by a property of B.

Min/Max Aggregators

Sometimes we need to limit assignments to a Cartesian product of entity-tags, based on some value, to [all but] the 𝑘 assignments for which the value is the lowest/highest. Here are some examples:

• Any person A and A’s five oldest offspring
• Any dragon and the three dragons it froze the largest number of times
• Any dragon and the four dragons it froze for the maximal cumulative duration

Three types are M aggregators are presented:

• M1: the value is the number of assignments to a union of Cartesian products of entity-tags
• M2: the value is the number of assignments to relationships/paths
• M3: the value is the evaluation result of an expression

M1 and M2 are syntactic sugar, which, alternatively, can be implemented by chaining A1 or A2 to an M3.

M1 Aggregator

Let 𝐵 denote a Cartesian product of one or more entity-tags. 𝐵 must be nonempty and must not be composed of entity-tags composing 𝑇.

Let 𝑀 denote a list of Cartesian products of entity-tags. 𝑀 must be nonempty and must not be composed of entity-tags composing 𝐵 or 𝑇.

The lower part of an M1 aggregator contains the following elements:

• optional: “all but”

• 𝑘: positive integer

• One of the following:
  • ‘et1 × et2 × …’: 𝐵 = et1 × et2 × …
  • ‘←’: 𝐵 = entity-tag directly left of the aggregator
  • ‘→’: 𝐵 = entity-tag directly right of the aggregator not wrapped with a negator nor preceded by a None quantifier (valid only when there is exactly one such entity-tag)
  • ‘⟷’: B = et1 × et2, where et1 is the entity-tag directly left of the aggregator, and there is a single entity-tag directly right of the aggregator not wrapped with a negator nor preceded by a None quantifier - et2

  Let BA(n) denote the list of all unique assignments to 𝐵 in S(n). BA(n)[o] is the o’th assignment.

• One of the following:
  • with min
  • with max
• One of the following (with min/max …):

  • ‘et11 × et12 × … ∪ et21 × et22 × … ∪ …’ (all products have the same arity):

    𝑀 = [et11 × et12 × … , et21 × et22 × … , …]

  • ‘←’:

    card(𝑀) = 1; 𝑀[1] = [et] where et is directly left of the aggregator

  • ‘→’:

    𝑀 = [et1, et2, …] where et1, et2, … are directly right of the aggregator and not wrapped with a negator nor preceded by a None quantifier (equivalent to ‘et1 ∪ et2 ∪ …’)

  • ‘⟷’:

    𝑀 = [et × et1, et × et2, …] where et is directly left of the aggregator and et1, et2, … are directly right of the aggregator and not wrapped with a negator nor preceded by a None quantifier (equivalent to ‘et × et1 ∪ et × et2 ∪ …’)

  Let MA(n, o, p) denote the list of all assignments to M[p] in the subset of S(n) that contains BA(n)[o].

  MC(n, o) = MA(n, o, 1) ∪ MA(n, o, 2) ∪ … - the set of unique assignments to elements in 𝑀 in the subset of S(n) that contains BA(n)[o].

For each 𝑛: from the set of assignments in S(n) - [all but] the 𝑘 assignments BA(n)[k] with the minimal/maximal positive card(MC(n, k)) are reported.

If there are only 𝑗<𝑘 assignments - all those 𝑗 are valid assignments. If there are 𝑗>𝑘 assignments with equal extremum - all those 𝑗 are valid assignments.

M1 location:

• Below a relationship/path

  A relationship/path with an M1 below may have a relationship/path-negator, and may be wrapped with ‘O’.

• Below a quantifier-input (excluding quantifier at the start of the pattern)

  A quantifier-input with an M1 below may be wrapped with an ‘O’ (except at the pattern’s start)

• Below the pattern’s start (even when followed by a quantifier)

  See Q299v1, Q299v2, Q262.

• If 𝑇 is empty - M1 appears directly right of the leftmost entity in 𝐵
• If 𝑇 is not empty and all the entities in 𝑇 appear right of all the entities in 𝐵: left of the rightmost entity in 𝑇. Otherwise: right of the leftmost entity in 𝑇
• If entities in 𝑇 ∪ 𝐵 are in different branches of a quantifier: directly left of the quantifier

Q67: The three people with the largest number of parents

Q68: The two dragons that were frozen by the largest number of dragons

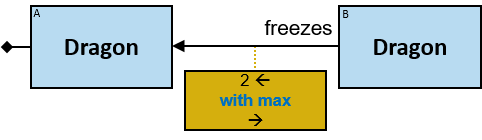
Q69: The two entities that own the largest number of entities

Q70: The five people who the number of people with a path of length up to four from each of them - is the smallest

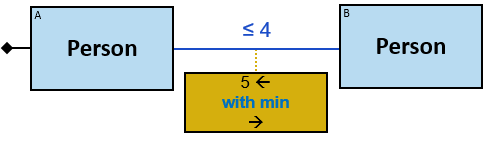
Q196: Any dragon owned by Brandon Stark and the three dragons it froze that froze the largest number of dragons

Q197: Any person A and A’s three dragons that the dragons they froze - froze the largest number of distinct dragons cumulatively

Q234: Any person and the three dragons whose dragons froze - that froze the largest number of dragons

Q236: Any person A and the three dragons whose dragons froze - that were frozen by the largest number of A’s dragons

Q227: Any dragon owned by Brandon Stark, and the three dragons it froze or fired at - that froze the largest number of dragons

Q238: For any pair of people (A, D) where A’s dragons froze D’s dragons - A’s three dragons that froze the largest number of D’s dragons

Q299: For any pair of people (A, E) where at least one of A’s dragons froze at least one of E’s dragons - A’s (up to) three dragons that cumulatively froze the largest number of E’s dragons (two versions)

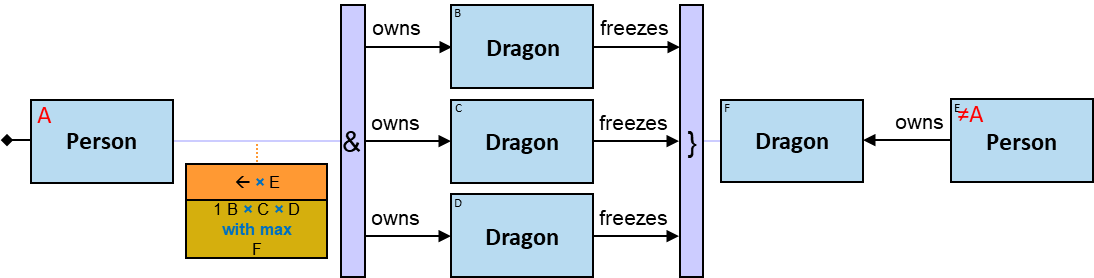
Note that the same graph-entity may be assigned to B, C, and D.

M2 Aggregator

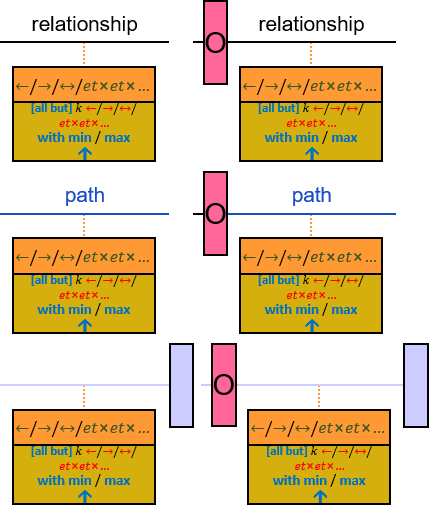
Let 𝐵 denote a Cartesian product of one or more entity-tags. 𝐵 must be nonempty and must not be composed of entity-tags composing 𝑇.

The lower part of an M2 aggregator contains the following elements:

• optional: “all but”

• 𝑘: positive integer

• One of the following:
  • ‘et1 × et2 × …’: 𝐵 = et1 × et2 × …
  • ‘←’: 𝐵 = entity-tag directly left of the aggregator (see Q78, Q171, Q172)
  • ‘→’: 𝐵 = entity-tag directly right of the aggregator not wrapped with a negator nor preceded by a None quantifier (valid only when there is exactly one such entity-tag) (see Q195, Q228)
  • ‘⟷’: 𝐵 = et1 × et2, where et1 is the entity-tag directly left of the aggregator, and there is a single entity-tag directly right of the aggregator not wrapped with a negator nor preceded by a None quantifier - et2 (see Q77, Q80)

  Let BA(n) denote the list of all unique assignments to 𝐵 in S(n). BA(n)[o] is the o’th assignment.

• One of the following:
  • with min ↑
  • with max ↑

  Let 𝑅 denote a list where each element is a pattern-relationship/pattern-path. 𝑅 must be nonempty.

  When M2 appears below a relationship/path - card(𝑅) = 1; R[1] = the relationship/path.

  When M2 appears below a quantifier-input - each element in 𝑅 is the relationship/path that follows one branch of the quantifier, excluding relationships/paths wrapped with a negator or a relationship/path-negator.

  Let RA(n, o, p) denote the list of all assignments to R[p] in the subset of S(n) that contains BA(n)[o].

  RC(n, o) = RA(n,o,1) ∪ RA(n, o, 2) ∪ … - the set of unique assignments to elements in 𝑅 in the subset of S(n) that contains BA(n)[o].

For each 𝑛: from the set of assignments in S(n) - [all but] the 𝑘 assignments BA(n)[k] with the minimal/maximal positive card(RC(n, o)) are reported.

If there are only j<k assignments - all those 𝑗 are valid assignments. If there are j>k assignments with equal extremum - all those 𝑗 are valid assignments.

M2 location:

• Below the relationship/path whose assignments are counted

  A relationship/path with an M2 below it may be wrapped with an ‘O’.

• Below a quantifier-input (except a None quantifier) that assignments to relationships/paths on its right are counted

  A quantifier-input with an M2 below it:

  • may be wrapped with an ‘O’
  • at least one branch of the quantifier (or subbranch of a sequence of quantifiers) must start with a relationship/path with no relationship/path-negator that is not wrapped with a negator nor preceded by a None quantifier

Q78: The four dragons that froze Balerion the largest number of times

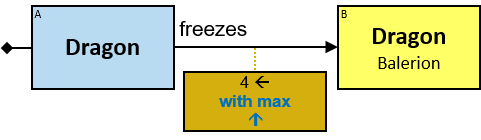
Q171: The two dragons that were frozen the largest number of times

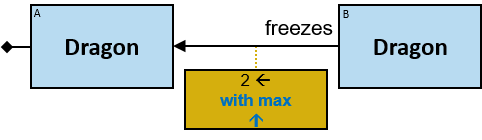
Q172: The five people with the smallest positive number of paths of length up to four to some person

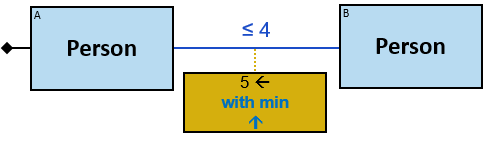
(Compare with Q324)

Q77: The five pairs of dragons (A, B) with the largest number of times B froze A

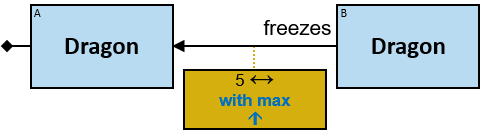
Q80: The three pairs of people with the largest number of paths of length up to four between them

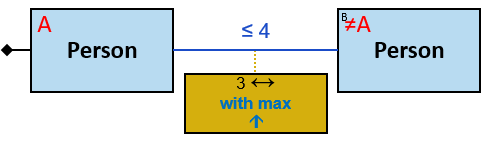
Q195: Any dragon owned by Brandon Stark and the three dragons it froze the largest number of times

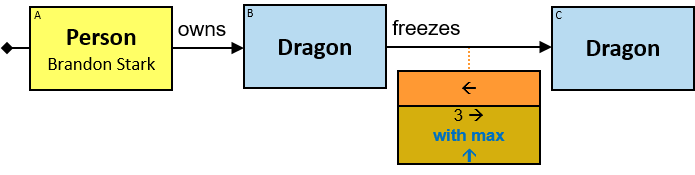
Q231: Any person A and the three dragons that were frozen by dragons that were frozen the largest number of times by A’s dragons

Q228: Any dragon owned by Brandon Stark that fired at at least two dragons, and the three dragons it fired the largest number of times

(counting the number of relationships assignments directly right of the quantifier)

Q237: For any pair of (A - a dragons owner, and C - a dragon that was frozen by A’s dragons) - the three dragons owned by A that froze C the largest number of times

Q239: For any pair of people (A, D) where A’s dragons froze D’s dragons - the three pairs of (A’s dragon B, D’s dragon C) where B froze C the largest number of times

M3 Aggregator

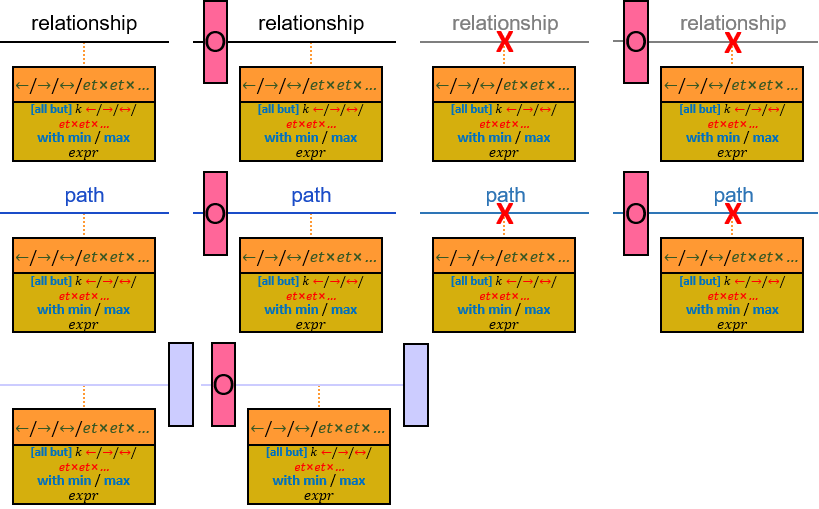
Let 𝐵 denote a Cartesian product of one or more entity-tags.

The lower part of an M3 aggregator contains the following elements:

• optional: “all but”

• 𝑘: positive integer

• One of the following:
  • ‘et1 × et2 × …’: 𝐵 = et1 × et2 × …
  • ‘←’: 𝐵 = entity-tag directly left of the aggregator
  • ‘→’: 𝐵 = entity-tag directly right of the aggregator not wrapped with a negator nor preceded by a None quantifier (valid only when there is exactly one such entity-tag)
  • ‘⟷’: 𝐵 = et1 × et2, where et1 is the entity-tag directly left of the aggregator, and there is a single entity-tag directly right of the aggregator not wrapped with a negator nor preceded by a None quantifier - et2

  Let BA(n) denote the list of all unique assignments to 𝐵 in S(n). BA(n)[o] is the o’th assignment.

• One of the following:
  • with min expr
  • with max expr

  expr is an expression composed of constants, properties, and subproperties of 𝑅 (when M3 appears below a relationship 𝑅 with no relationship-negator) (see Q74), EA-tags defined on top of the aggregator (see Q91, Q274, Q306), and EA-tags defined right of the aggregator (see Q130, Q128)

  Let RA(n, o) denote the minimal/maximal assignment to expr in the subset of S(n) that contains BA(n)[o].

For each 𝑛: from the set of assignments in S(n) - [all but] the 𝑘 assignments BA(n)[k] with the minimal/maximal RA(n, k) are reported.

If there are only j<k assignments - all those 𝑗 are valid assignments. If there are j>k assignments with equal extremum - all those 𝑗 are valid assignments.

M3 location:

• Below a relationship/path

  When M3 appears below a relationship 𝑅, and expr is composed of at least one property or subproperty of 𝑅, 𝑅 may be wrapped with an ‘O’. Otherwise - a relationship or path with an M3 below it may have a relationship/path-negator and may be wrapped with an ‘O’.

• Below a quantifier-input (excluding quantifier at the start of the pattern)

  A quantifier-input with an M3 below it may be wrapped with an ‘O’.

• Below the pattern’s start (even when followed by a quantifier)

  See Q130, Q216, Q264.

• If 𝑇 is empty - M3 appears directly right of the leftmost entity in 𝐵
• If 𝑇 is not empty and all the entities in 𝑇 appear right of all the entities in 𝐵: left of the rightmost entity in 𝑇. Otherwise: right of the leftmost entity in 𝑇
• If entities in 𝑇 ∪ 𝐵 are in different branches of a quantifier: directly left of the quantifier

Q130: The four oldest people

Q131: The four oldest males

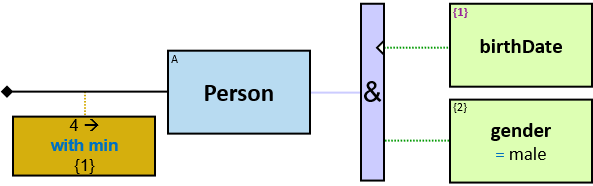
Q118: Any person A and A’s three oldest offspring

Q119: Any person A and A’s three youngest sons

Q74: Any person A and A’s three horses with the minimal first ownership start date

Q230: Any person A and the three people A is a friend of or a friend of an offspring of - that own the heaviest horses

Q232: Any person A and the three heaviest horses owned by people A is a friend of or a friend of an offspring of

R1 Aggregator

Let 𝑅 denote the relationship R1 appears below it.

The lower part of an R1 aggregator contains the following elements:

• optional: “all but”
• 𝑘: positive integer
• ‘↑’ (an arrow pointing to the relationship on top of the aggregator):
• One of the following:
  • with min relExpr
  • with max relExpr

  relExpr is an expression containing at least one property or subproperty of 𝑅

  Let RA(n) denote the list of all unique assignments to 𝑅 in S(n). RA(n)[o] is the o’th assignment.

For each 𝑛: from the set of assignments in S(n) - [all but] the 𝑘 assignments RA(n)[k] with the minimal/maximal relExpr are reported.

If there are only j<k assignments - all those 𝑗 are valid assignments. If there are j>k assignments with equal extremum - all those 𝑗 are valid assignments.

R1 location:

• Below the relationship whose property is referenced

  The relationship may be wrapped with an ‘O’.

Q241: The four longest freezes

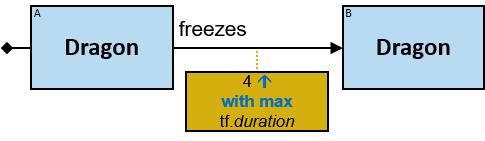
Q161: For each dragon that froze at least one dragon at least once: the four longest freezes

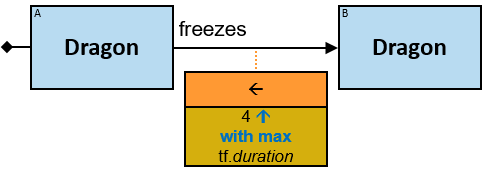
Q160: For each pair of dragons (A, B) where A froze B at least once: The four longest freezes

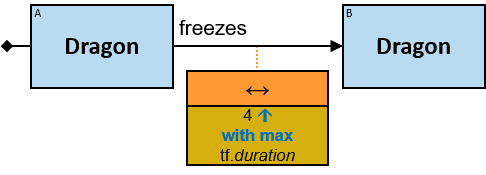
Q240: For any pair of people (A, D): The four longest freezes where any of A’s dragons froze any of D’s dragons

Aggregator Chains

Relationships’ expressions and aggregators can be chained. When chained, each relationship’s expression and each aggregator with a constraint is a filtering stage. An assignment is valid only if all the chained constraints are satisfied, or in other words - if it passed all filtering stages.

Within a chain, relationships’ expressions may not appear below aggregators. Also, an aggregator may not appear in a horizontal quantifier’s branch. It may appear below a horizontal combiner that combines all the branches (see Q302, Q303).

Q96: Any dragon Balerion froze more than ten times - each on or after January 1, 1010, and for a duration shorter than ten minutes

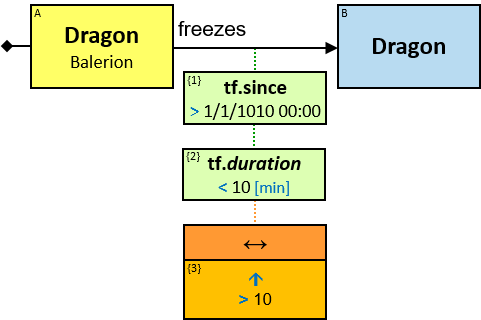
Note that the order of the constraints along the chain matters: the top two constraints filter relationships based on their properties’ value. The third constraint is on the number of relationships that passed these filters.

Q302: Any dragon A that froze at least three dragons - each at least one time where at least two of the following conditions are satisfied: (i) the freeze duration was longer than ten minutes (ii) the freeze started after January 1, 980 (iii) the freeze ended before February 1, 980

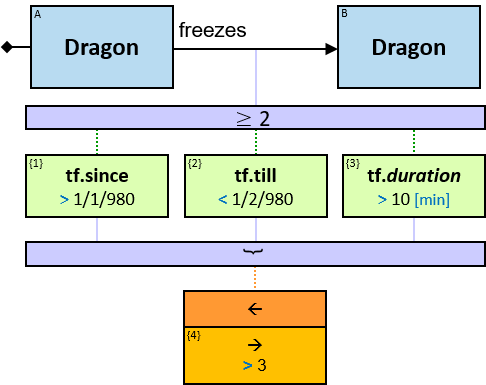
See Q185 for a different pattern structure that could be used.

Q303: Any pair of dragons (A, B) where A froze B at least three times, each for more than ten minutes, and either the freeze started after January 1, 980 or ended before February 1, 980

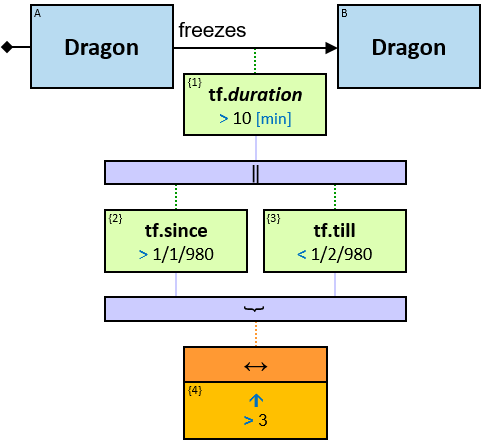
Q186: Any dragon Balerion froze more than ten times for less than ten minutes, and at least once for ten minutes or more

Q99: Any dragon Balerion froze more than ten times for less than ten minutes, and not once for ten minutes or more (two versions)

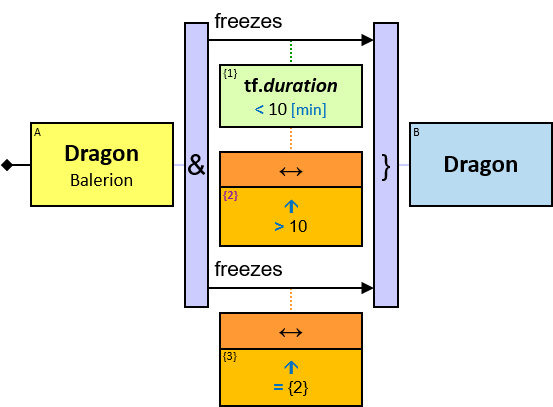
Q94: Any dragon that froze more than three dragons: each more than five times for more than ten minutes

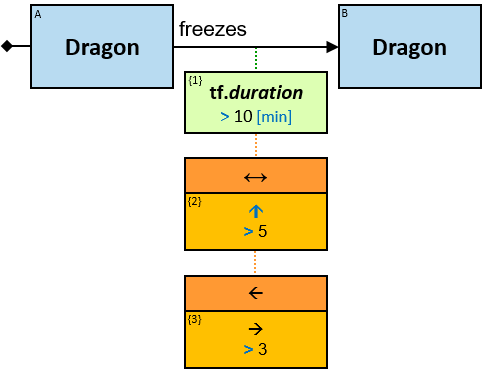
Filtering stages:

• Pass freezes longer than ten minutes
• Pass pairs of dragons (A, B) where A froze B more than five times for more than ten minutes
• Pass dragons A that froze more than three B’s each more than five times for more than ten minutes

Q93: Any dragon A that froze more than three dragons - each at least five times for more than ten minutes

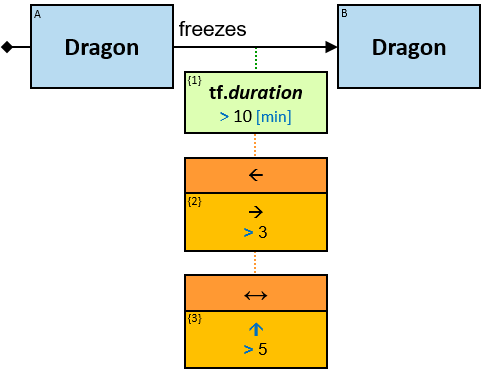
(Similar to Q94, but the order of the aggregators is switched.) Filtering stages:

• Pass freezes longer than ten minutes
• Pass dragons A that froze more than three B’s - each at least once for more than ten minutes
• Pass pairs of dragons (A, B) where A froze B more than five times for more than ten minutes

A dragon A that froze more than three dragons, each at least once for more than ten minutes, but froze only a single dragon more than five times for more than ten minutes - is a valid assignment in Q93 but not in Q94.

Q272: Any pair of dragons (A, B) where the longest freeze duration is at least ten times longer than the shortest freeze duration

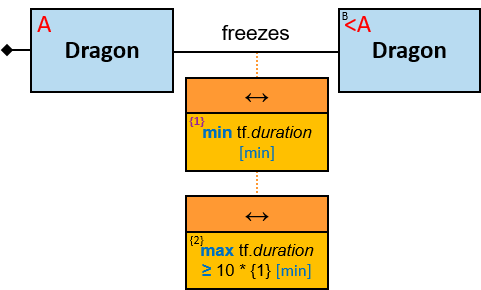
Q363: Any dragon that the latest time it froze some dragon for the first time was in or after 1010

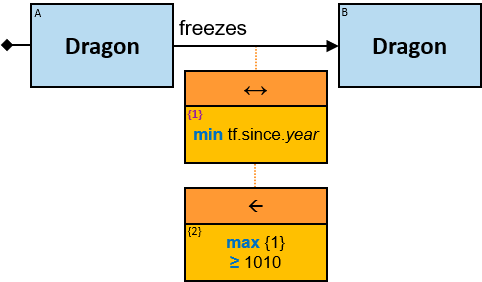
Q91: The four dragons with the maximal (shortest duration they were frozen for)

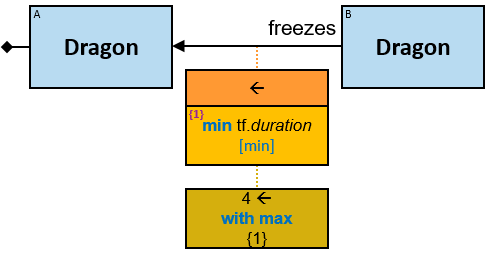
Q90: The four pairs of dragons (A, B) where A froze B for the maximal cumulative duration

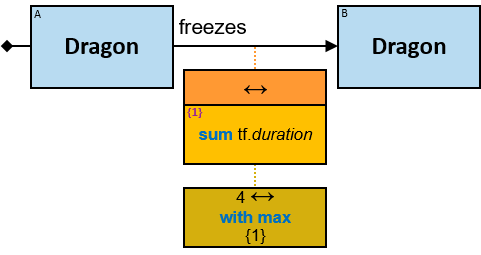
Q92: The four dragons with the maximal (average duration they froze dragons for)

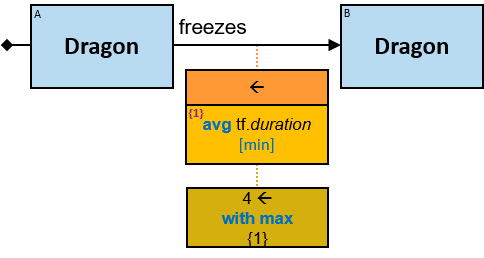
Q201: For each dragon that froze at least ten dragons: the three dragons it froze for the maximal cumulative duration

Q274: The four dragons with the largest difference between (the longest duration they froze dragon for) and (the shortest duration they froze dragon for)

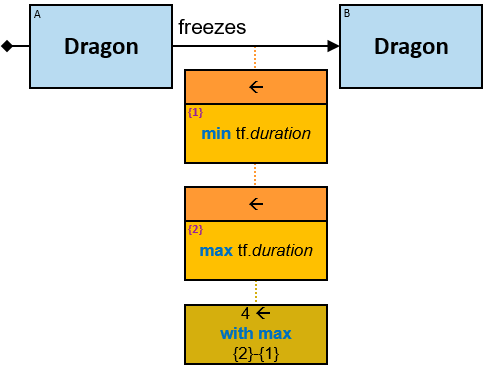
Q182: Any dragon owned by Brandon Stark and the three dragons it froze for the maximal cumulative duration

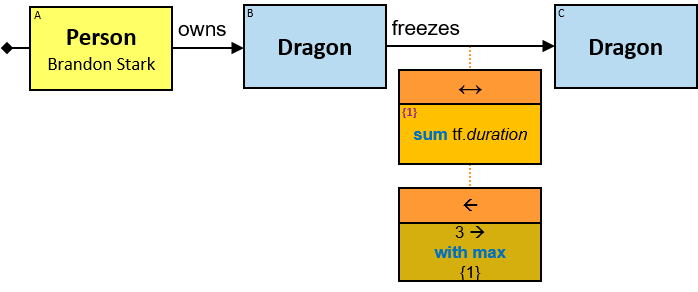
Q133: The four people that the average weight of their horses is maximal

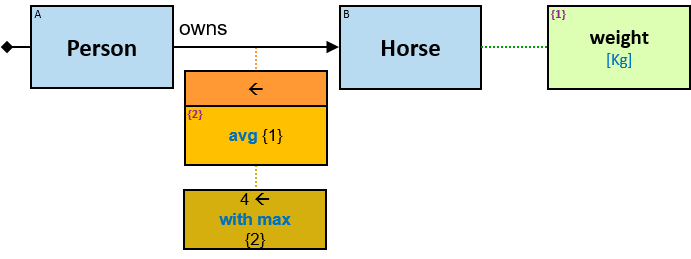
Q132: The four people who own horses of the largest number of colors

Q233: Any dragon A than froze dragons Bs that froze dragons Cs, and the three Cs for which A froze Bs for the maximal cumulative duration

Q138: The four people who the people each of them is a friend of - cumulatively own horses of the largest number of colors

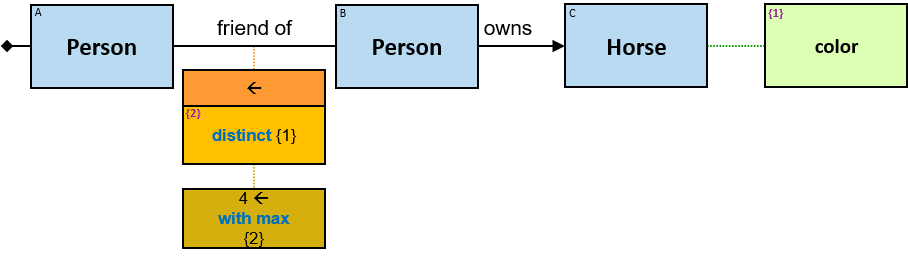
Q183: The three dragons that dragons owned by Brandon Stark froze for the maximal cumulative duration

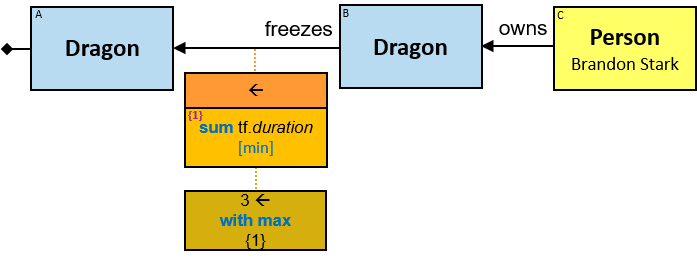
Q168: The three people who the number of types of entities each of them owns is the largest

Q163: Any dragon that the average duration of the ten shortest times it froze dragons is longer than 60 minutes

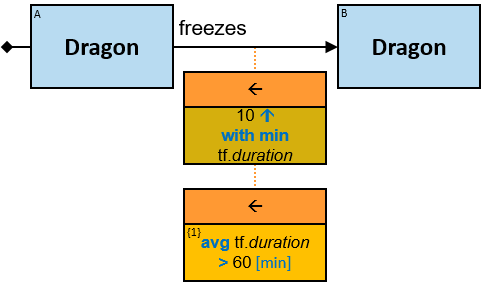
Q162: Any pair of dragons (A, B) where the second shortest duration A froze B is longer than 60 minutes

Q341: For each pair of dragons (A, B): the two shortest freezes A froze B. If there are more than two freezes with equal minimal duration - the two earliest amongst them

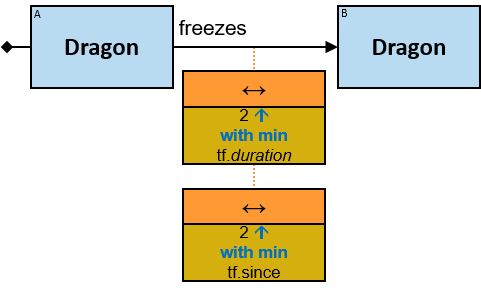
Q268: Any pair of dragons (A, B) where the average duration of the 11th-20th most prolonged freezes A froze B is longer than 60 minutes (two versions)

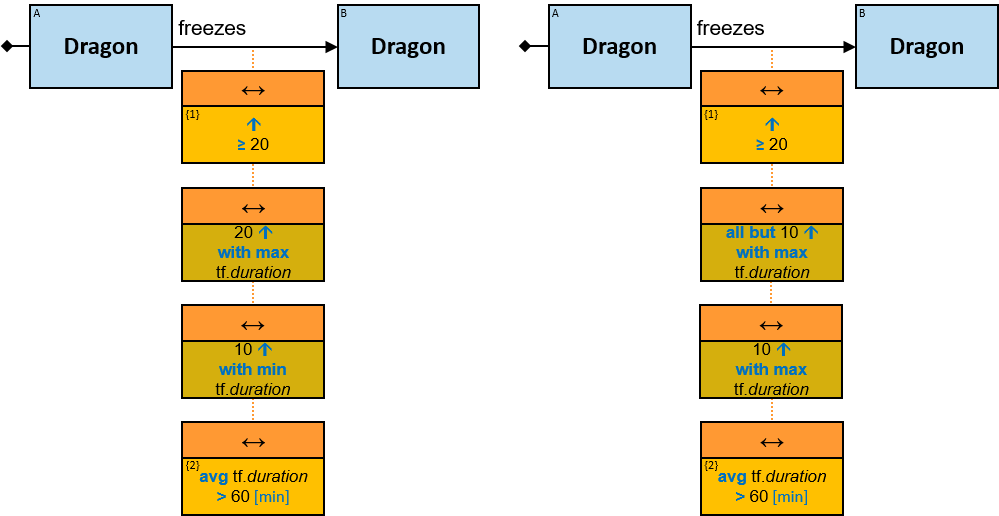
Q120: Any person A whose three oldest offspring’s cumulative height is lower than A’s height

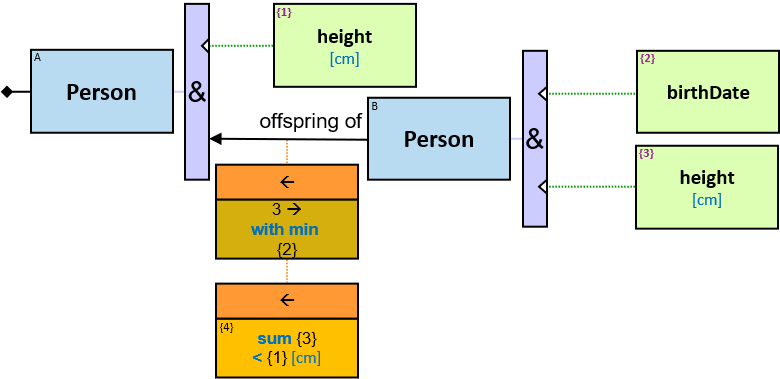
Q202: Any person A whose three oldest offspring’s average height is lower than the average height of all A’s offspring

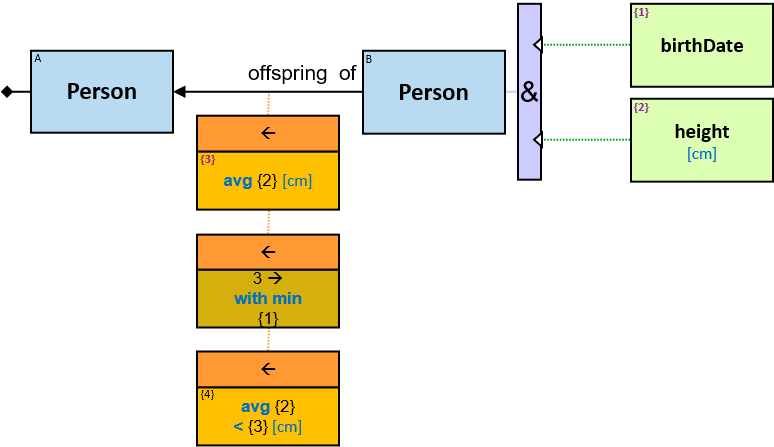
Q208: Any person whose three oldest horse-owning sons cumulatively own horses of three colors

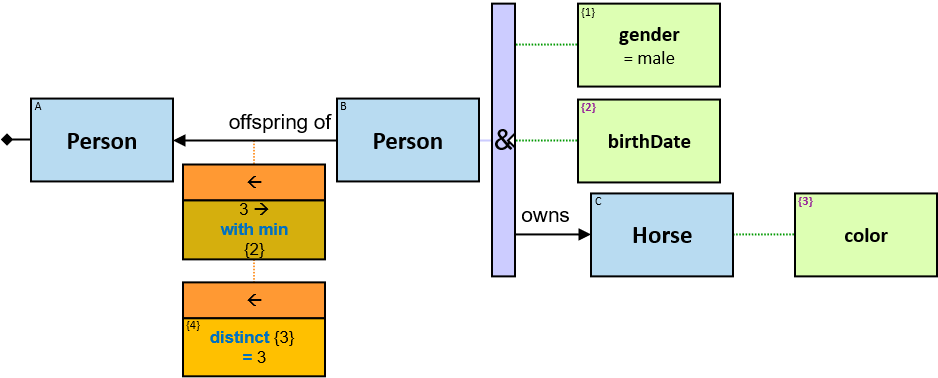
Q140: Any person whose three oldest sons cumulatively own horses of three colors

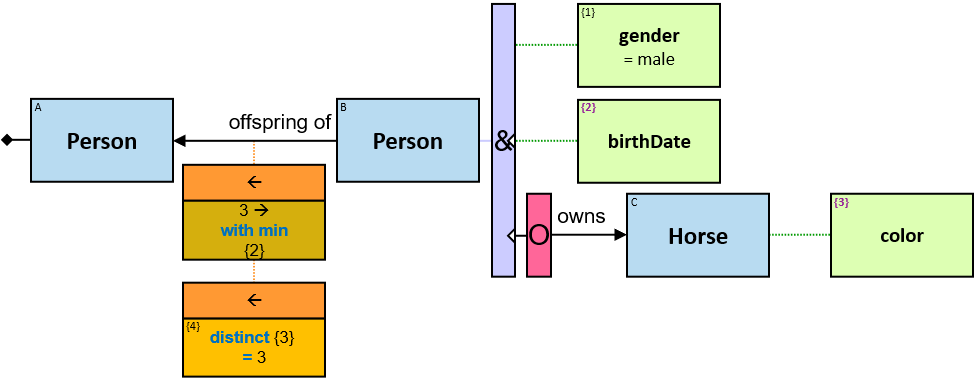
Note that {3} is defined right of an ‘O’ and is evaluated to null when the optional part has no valid assignment. distinct does not aggregate null evaluation results.

Q141: Any person A whose three oldest sons cumulatively own horses of the same number of colors as of those cumulatively owned by A’s three youngest daughters

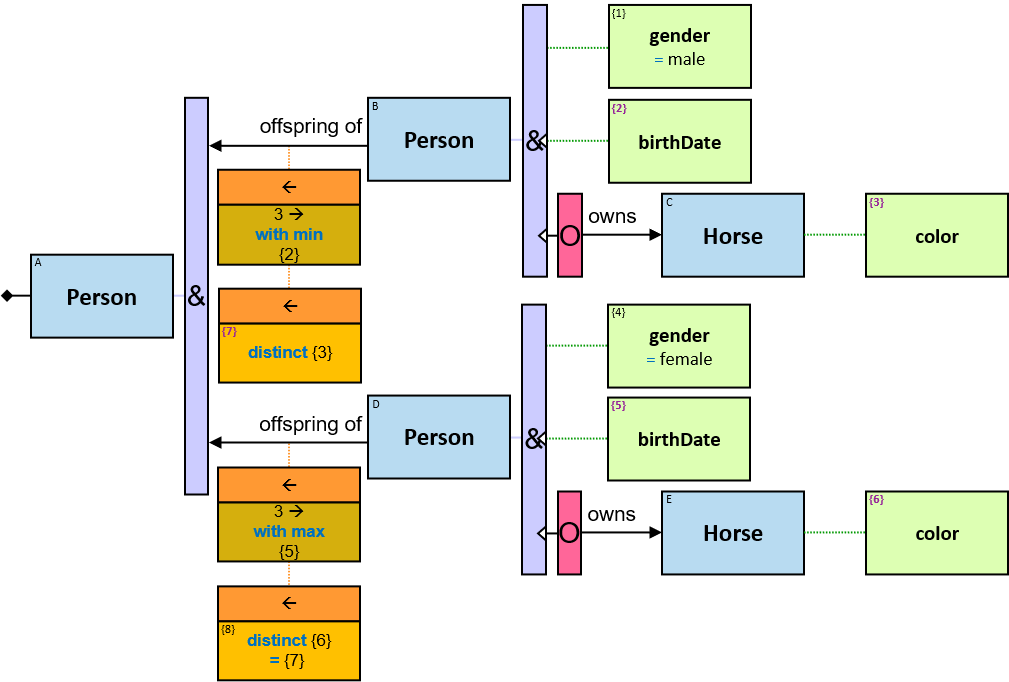
Q95: Any dragon Balerion froze more than five times, each for more than ten minutes, and the total duration of those freezes was longer than 100 minutes (three versions)

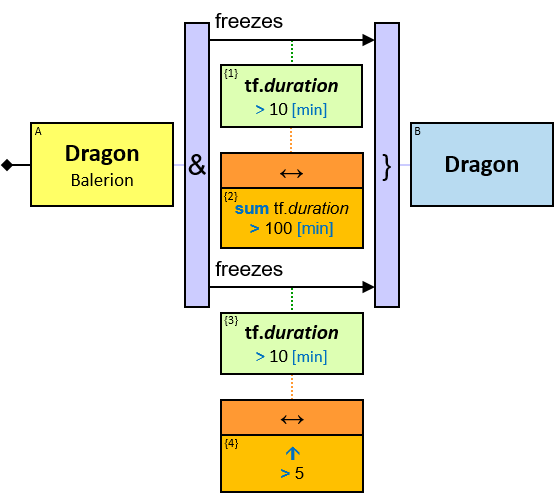
The two per pair constraints could be chained instead. The meaning would be similar:

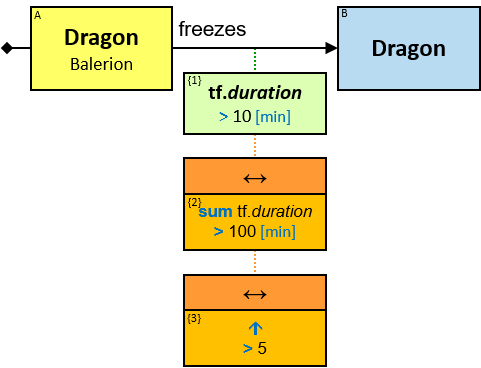
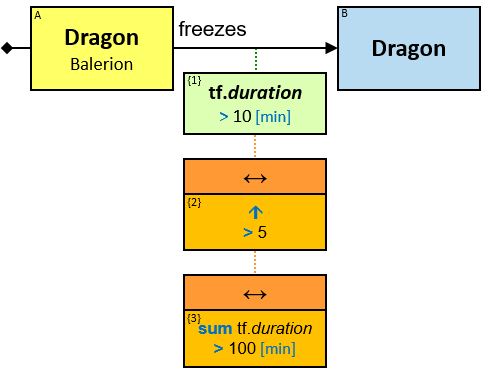
Q199: Any dragon that (froze more than ten times each of more than ten dragons) and (froze more than 20 times each of less than ten dragons)

Q200: Any dragon that (froze more than ten times each of more than ten dragons. For each of these ten dragons - the freezes had exactly two distinct durations) and (froze more than 20 times each of less than ten dragons. The average freeze duration of all these dragons - is longer than three minutes)

Q277: Any dragon that the longest (cumulative duration it froze some dragon) is more than ten times longer than the shortest (cumulative duration it froze some dragon)

Q351: Any person who owns two horses of different colors, a dragon that froze at least ten dragons of the same color as the first horse, and a dragon that froze at least ten dragons of the same color as the second horse

Q320: Any person A where there are more horses of the same colors as A’s owned horses than dragons of the same colors as A’s owned dragons (version 1)

The number of assignments to E is zero when the optional part has no assignment. We cannot simply test if E < {5} since if there are zero assignments to E per A - the constraint is not satisfied.

Q321: Any person A where more horses than dragons have the same name-length as a horse/dragon A owns (version 1)

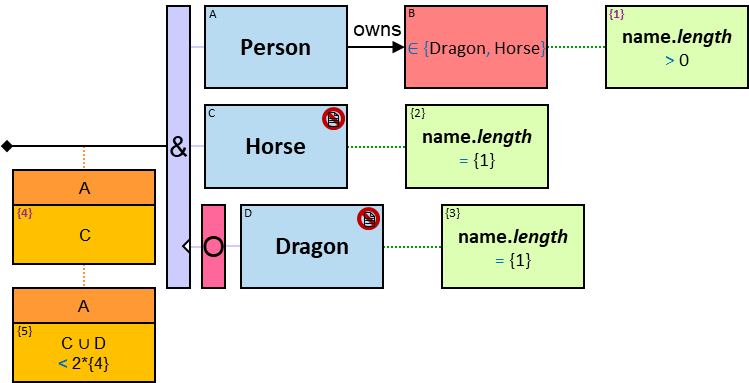
The number of assignments to D is zero when the optional part has no assignment. We cannot simply test if D < {4} since if there are zero assignments to D per A - the constraint is not satisfied.

Q259: Any person who since 1011 become an owner of no horses or up to four horses (two versions)

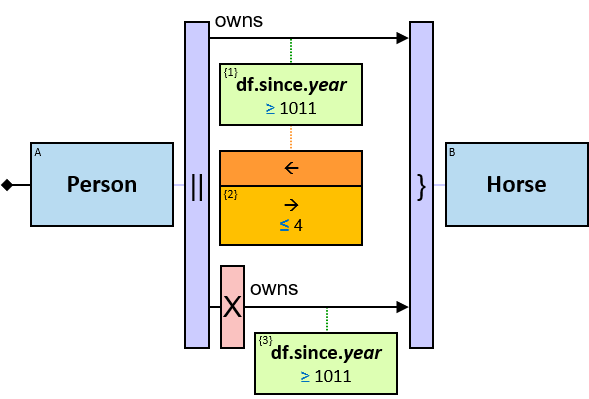
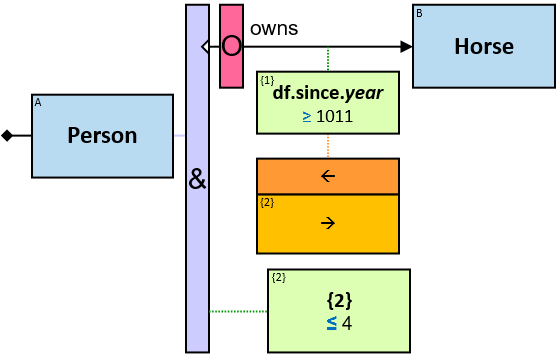
Q337: For each pair of dragons: each time one of them froze the other for a duration longer than the average duration of all the freezes that are longer than the average duration one of them froze the other

Q317: Any dragon that the time difference between the earliest time it froze/fired at some dragon and the latest time it froze/fired at some dragon - is at least one year

{1}, {2}, {3} and {4} are defined right of an ‘O’, hence evaluated to null when the optional part has no assignments. Since min({…}) and max({…}) ignore nulls, the pattern would yield the expected results even when dragon A froze no dragon or when dragon A fired at no dragon.

Q377: Any dragon and the three earliest times it froze/fired at some dragon

{1} and {2} are defined right of an ‘O’, hence evaluated to [] when the optional part has no assignments.

Aggregator Sequences

Multiple aggregators may appear along a sequence. Along a sequence, aggregator’s constraints are evaluated from right to left, except where a constraint depends on the evaluation result of a constraint on its left (see Q376).

Q128: Any person A and A’s three offspring who own horses of the largest number of colors

Q198: Any person A and A’s three dragons that (for each of them: the four dragons it froze that froze the largest number of dragons) - froze the largest number of distinct dragons cumulatively

Q328: The three people with the maximal cumulative horse ownership days

Q179: Any pair of dragons (A, B) where A froze B for a cumulative duration longer than the cumulative duration B froze dragons (two versions)

Q103: Any dragon A that froze at least three dragons, each of which was frozen by at least four dragons other than A

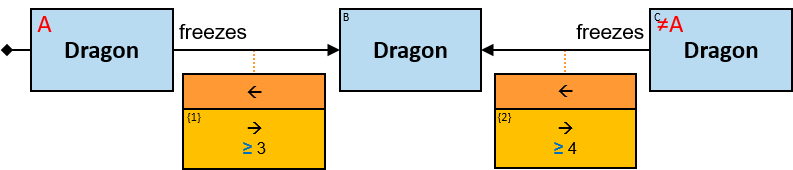
Q106: Any dragon A that froze dragons at least three times - each was frozen at least four times by dragons other than A

Q164: Any dragon that the number of times dragons it froze have frozen dragons (cumulatively) - is equal to the number of times dragons it fired at have fired at dragons (cumulatively)

Q356: The average number of horse ownerships per person

Q324: The five people with the smallest number (including zero) of paths of length up to four to some person

(Compare with Q172)

Q107: Any dragon that (the number of dragons, each owned by five people, that froze it) is five, and that the number of times it was frozen by those dragons (cumulatively) is not five

Q169: Any person A who (has at least one offspring who owns at least three horses) and (each of A’s offspring who owns at least three horses - owns horses of at least three colors)

Q129: Any person A that (each of A’s offspring who owns at least one horse - owns a different number of horses)

Q181: Any dragon with no intersection between the groups of dragons frozen by any two dragons it froze

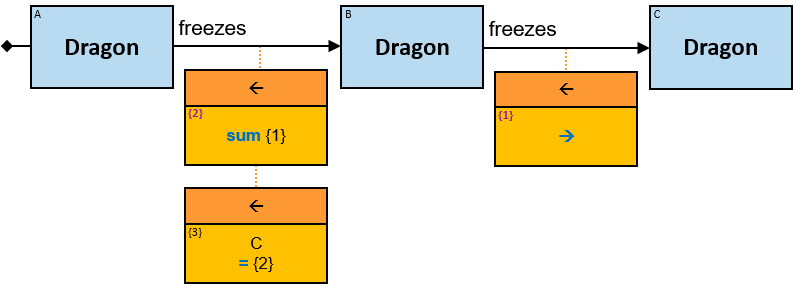
Q213: Out of the pairs of dragons (A, B) where A froze B for a cumulative duration longer than the cumulative duration B froze dragons - the five pairs with the largest number of times A froze B

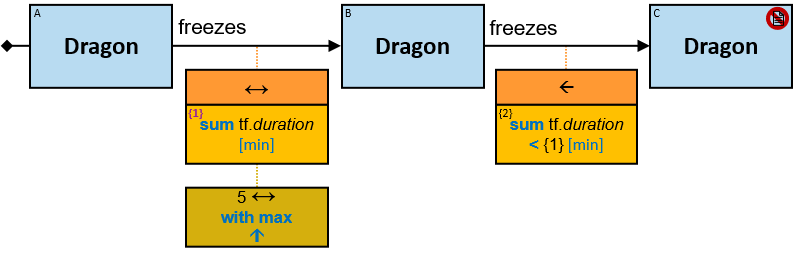
When the order of the aggregators along the chain is switched, the meaning changes:

Q376: Out of the five pairs of dragons (A, B) with the largest number of times A froze B – the pairs where A froze B for a cumulative duration longer than the cumulative duration B froze dragons

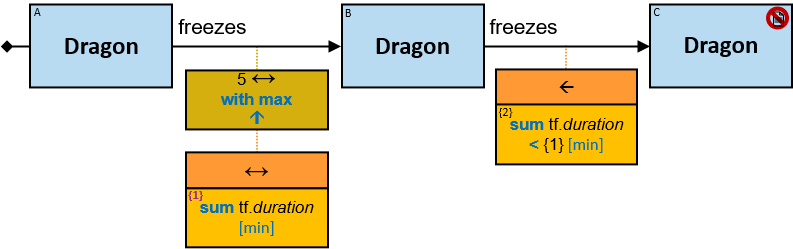
Since {2} has a constraint that depends on the evaluation of {1}, {1} must be evaluated first. However, the M2 aggregator filters (A, B) pairs before {1} is evaluated.

Q191: Any dragon that froze dragons S and fired at dragons T. |S|≥3, |T|≥3 and |S∪T|≥10

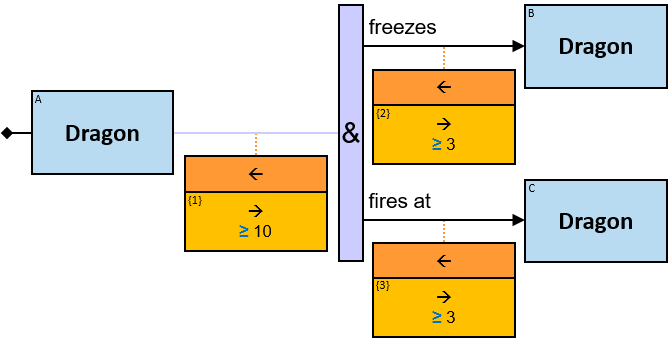
Q192: Any dragon that froze dragon m≥3 times and fired at dragons n≥3 times. m+n≥10

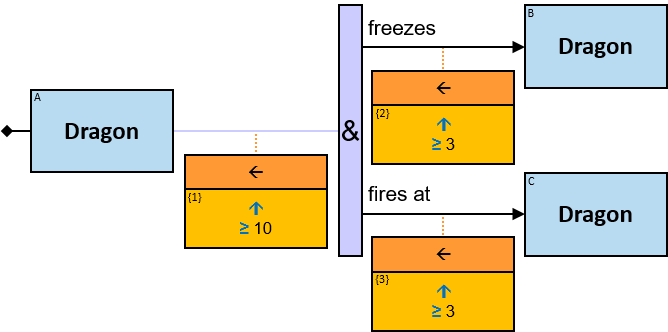
Q193: Any dragon that froze dragons S, fired at dragons T, and fired ≥3 times. |S|≥3 and |S∪T|≥10

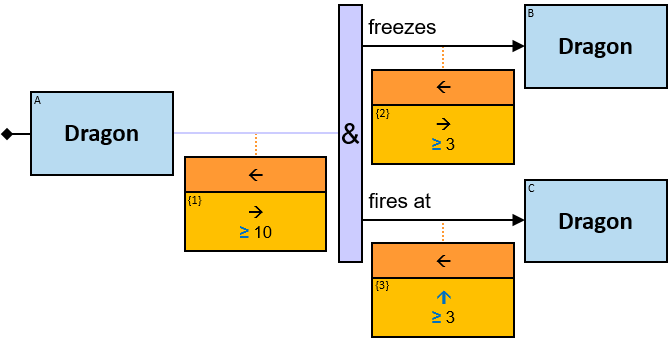
Q194: Any dragon that froze dragons m times, fired at dragons n≥3 times, and froze ≥3 dragons. m+n≥10

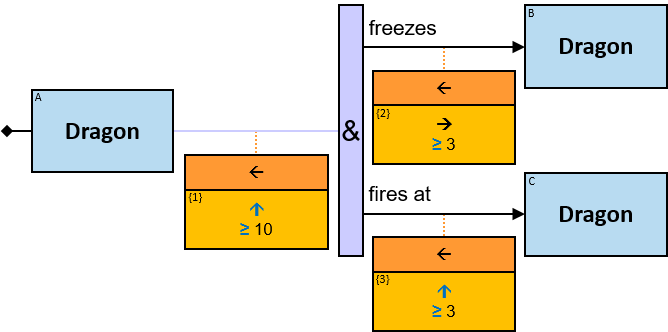
Q97: Any dragon that froze more than three dragons - each more than ten times or for a cumulative duration of more than 100 minutes

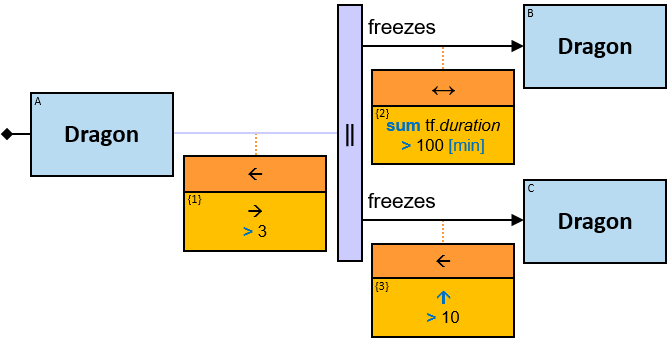
Q180: Any pair of dragons (A, B) where the cumulative duration A and B froze each other - is longer than both the cumulative duration A froze other dragons and the cumulative duration B froze other dragons

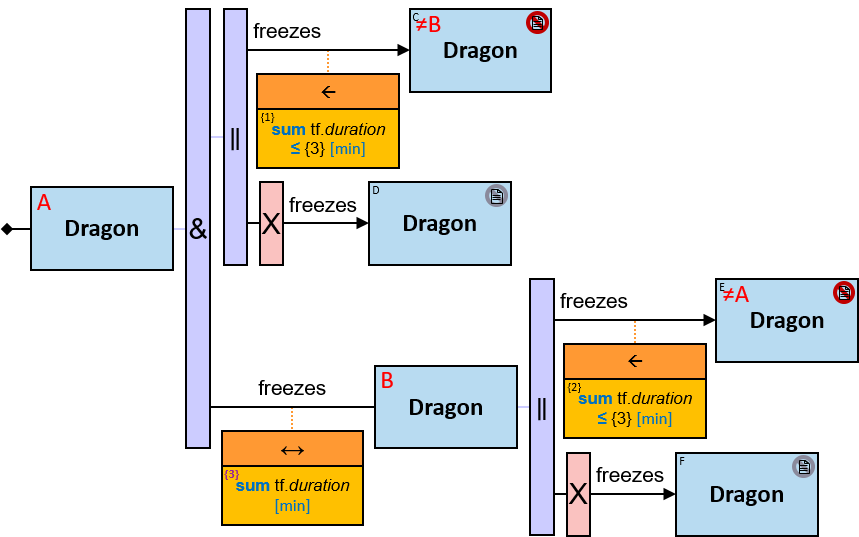
Q347: The five dragon triplets with the largest number of times triplet-members froze one another

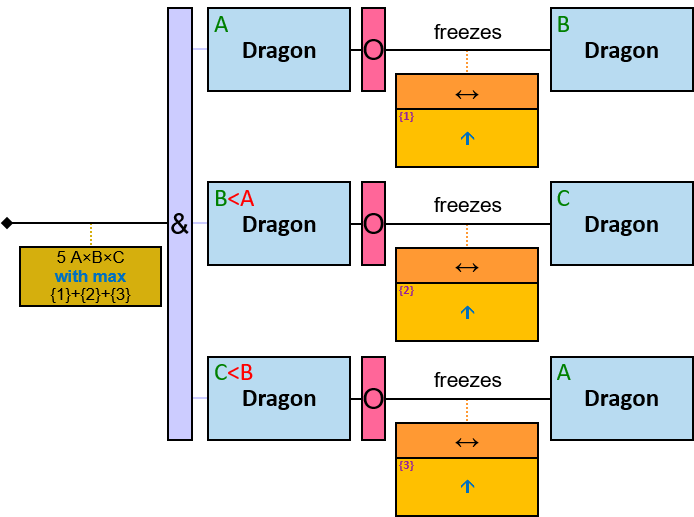
Note that we need to count each triplet only once (ignoring permutations).

Q100: Any dragon Balerion froze more than ten times for less than ten minutes, more than ten times on or after January 1, 1010, more than 15 times for less than ten minutes or on or after January 1, 1010, and more than 100 times altogether

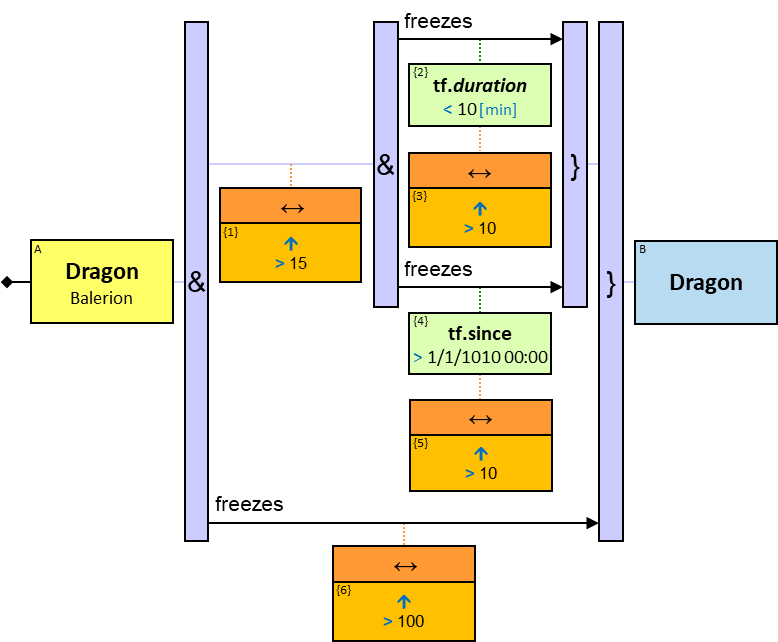
Extended Aggregators

For extended aggregators, 𝑇 denotes an extended Cartesian product - a Cartesian product not just of entity-tags but of

• Zero or more entity-tags
• Zero or more expressions, each can be either
  • an inherent property of the attached relationship
  • an EA-tag
• Zero or more entity type-tags
• Zero or more relationship type-tags

Hence, for all extended aggregator types (A1, A2, A3, M1, M2, M3, and R1), the per clause has the following format:

• ‘et1 × et2 × … × expr1 × expr2 × … × ⟨ ett1 ⟩ × ⟨ ett2 ⟩ × … × ⟪ rtt1 ⟫ × ⟪ rtt2 ⟫ × …:

  𝑇 = et1 × et2 × … × expr1 × expr2 × … × ⟨ ett1 ⟩ × ⟨ ett2 ⟩ × … × ⟪ rtt1 ⟫ × ⟪ rtt2 ⟫ × …

Wherever possible, the notations ‘←’, ‘→’ and ‘⟷’ are used instead of entity-tags.

For all extended M aggregators (M1, M2, and M3), the same is true also for 𝐵.

Here are two examples:

First example: Any person who at a certain date became an owner of more than five horses (Q115v2)

{1} is evaluated per each unique assignment to A × df.since in 𝑆. In other words, {1} is a property of each unique assignment to A × df.since in 𝑆.

Second example: For each color of dragons that Balerion froze - the three dragons it froze the largest number of times (Q215)

Extended A1 Aggregator

Q261: Any color of which there are at least ten horses

{2} is a property of each unique assignment to {1} in 𝑆.

Q115: Any person who at a certain date became an owner of more than five horses (two versions)

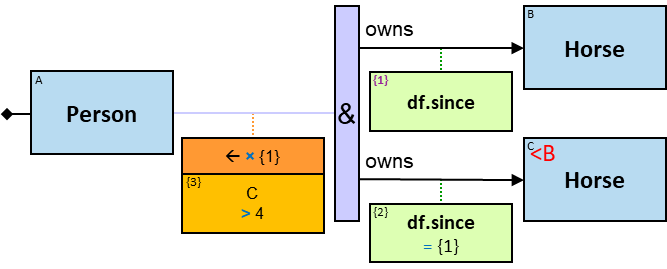
{1} is a property of each unique assignment to A × df.since in 𝑆.

Q289: Any person who at a certain three-day interval became an owner of more than five horses

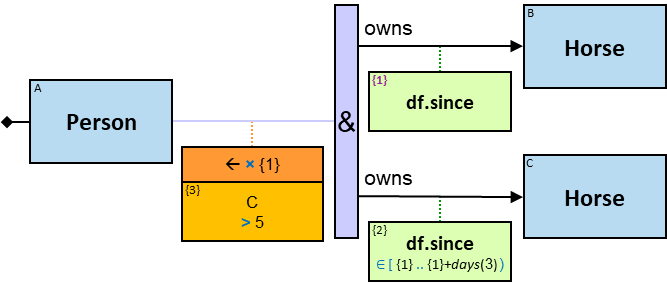
When 𝑛 intervals overlap, the intersection contains the start-time of at least one of the intervals (it also contains the end-time of at least one of the intervals).

Q283: Any person who at a certain day owned at least five horses

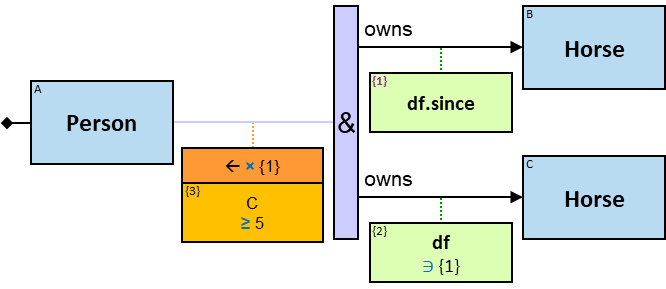
Q284: Any person who owned the same five horses - for at least ten consecutive days (version 1)

Q378: Any relationship-type that holds between more than 1000 pairs of dragons

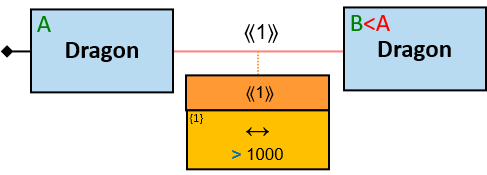
Q217: Any dragon and the dragons it froze - on days it froze between one and five dragons

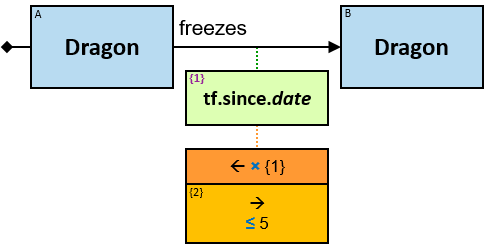
Q114: Any person who owns at least five horses of the same color (version 3)

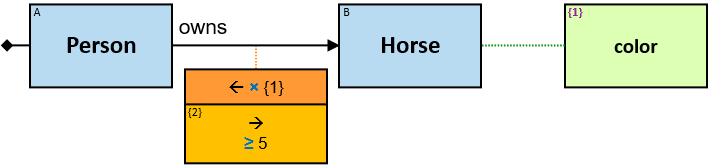
Q218: Any person who owns at least five entities of the same type (version 2)

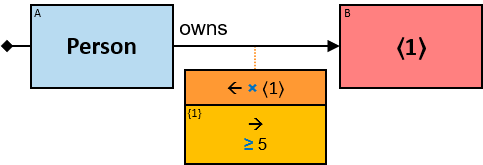
Q157: Any person who owns between one and three horses of the same color - for at least six colors

Q214: Any person who owns entities of at least four types. For each type - at least five entities

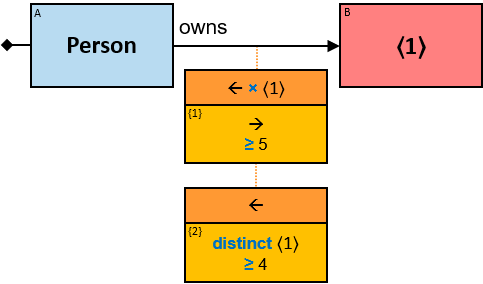
Q235: Any dragon that the number of dragons it froze on average - on months it froze dragons in - is at least ten

Q153: Any dragon A that in each of at least 11 days - froze between one and five dragons

Q252: Any dragon B that in each of at least 11 days - was frozen by a dragon that on that day froze between one and five dragons

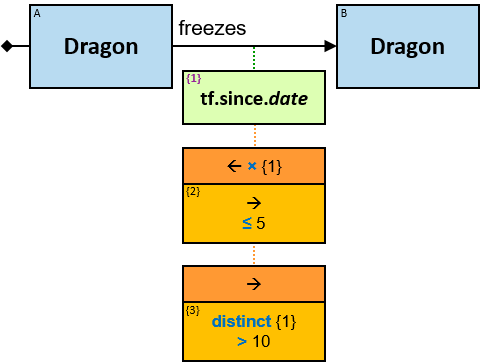
Q255: Any dragon whose name-length is equal to the number of days in each of which it froze ten dragons

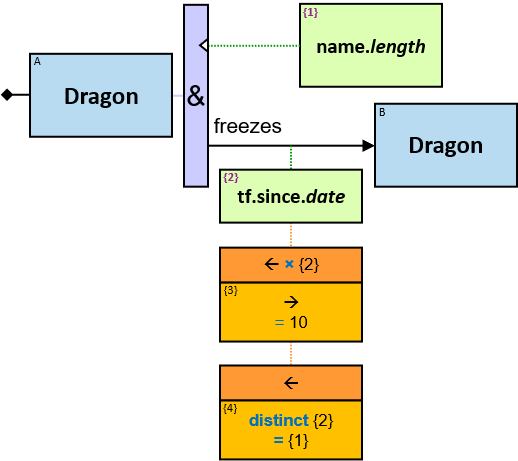
Q278: Any pair of dragons (A, B) that in each of at least 11 days - A froze between one and five dragons, one of them is B

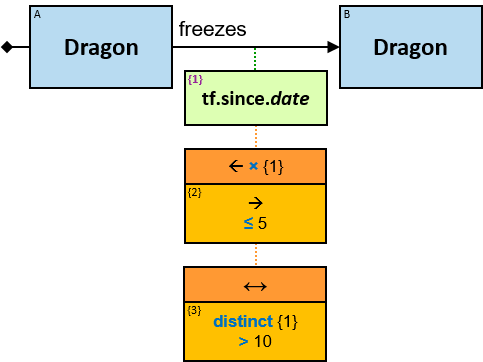
Q254: Any dragon that in each year it froze dragons - it froze more than three dragons

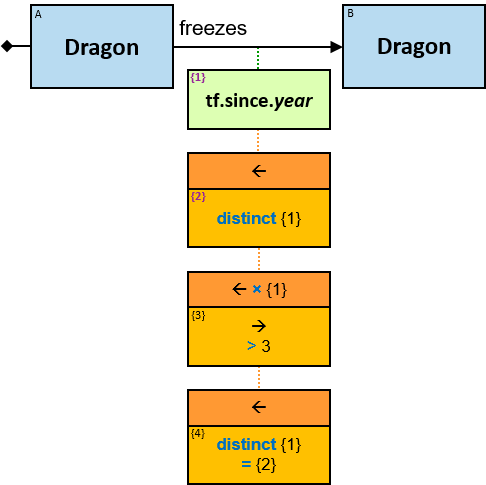
Q306: The three dragons that the number of days in each of which each froze at least five dragons - is maximal

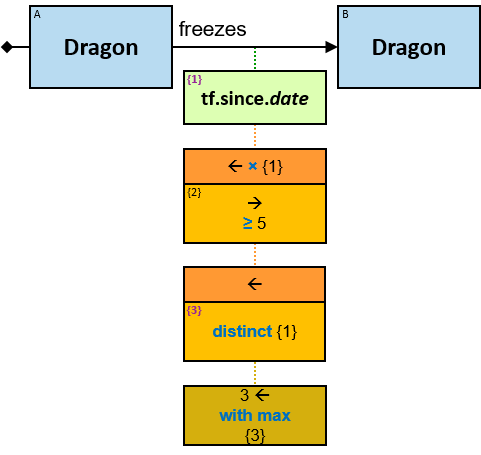
Q285: Any person who at a certain day owned at least five horses and at least five dragons

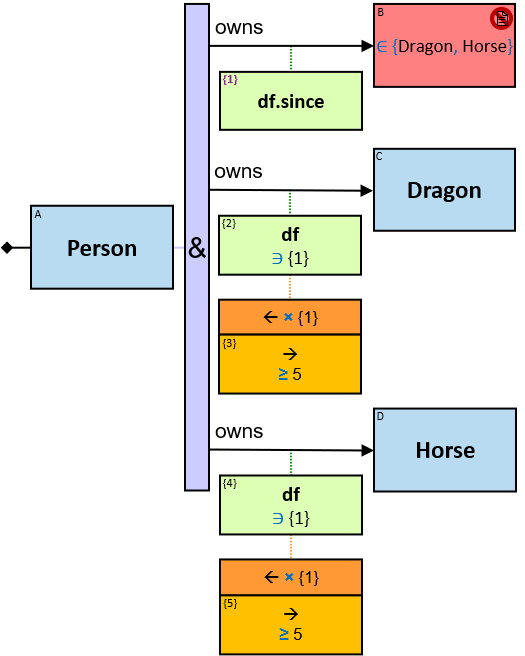
Q286: Any person who at each day of at least ten (not necessarily consecutive) days - owned at least five horses (not necessarily the same horses each day)

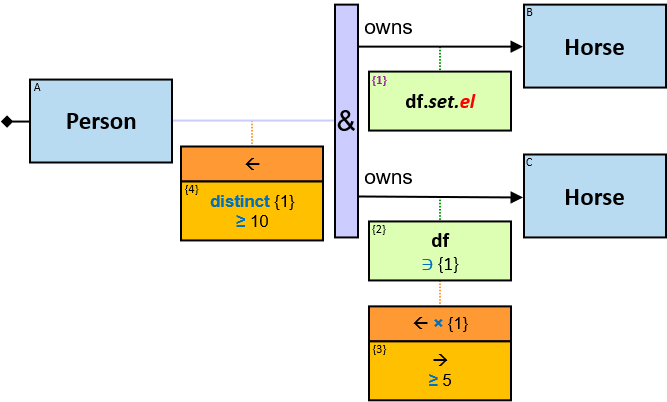
Q158: Any dragon that in each of at least ten days - the number of dragons it froze is greater than the number of dragons that froze it

Note the location of {6}. If it was below {1}, the evaluation order was different. As it is, {6} counts distinct assignments to {1} for which the All quantifier was satisfied.

Q260: Any dragon that in each of at least ten days: (i) the number of dragons it froze is greater than the number of dragons that froze it, and (ii) it froze/was frozen at least five times

Q350: Any pair of people who own the same number of entities of each type

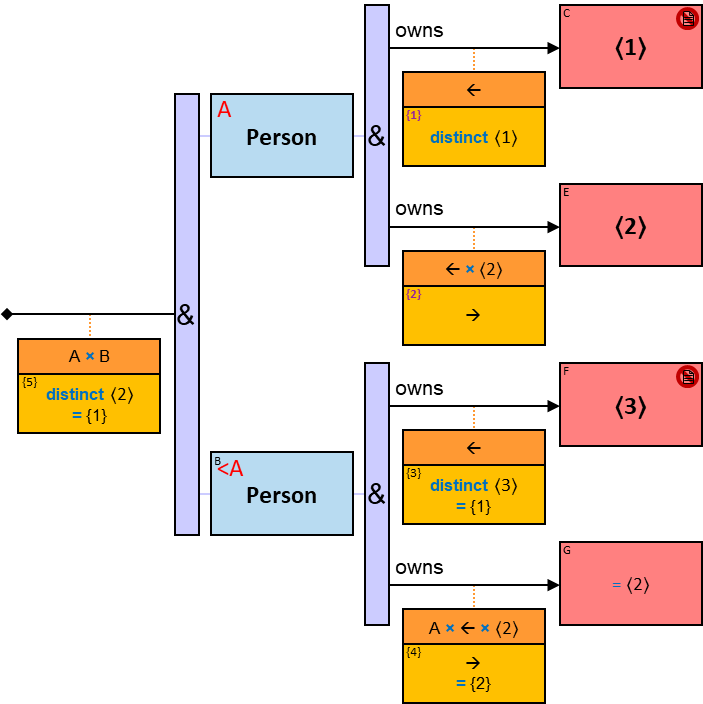
Q332: Any person whose horses are all of rare colors. A rare color is a color of less than 1% of the horses (two versions)

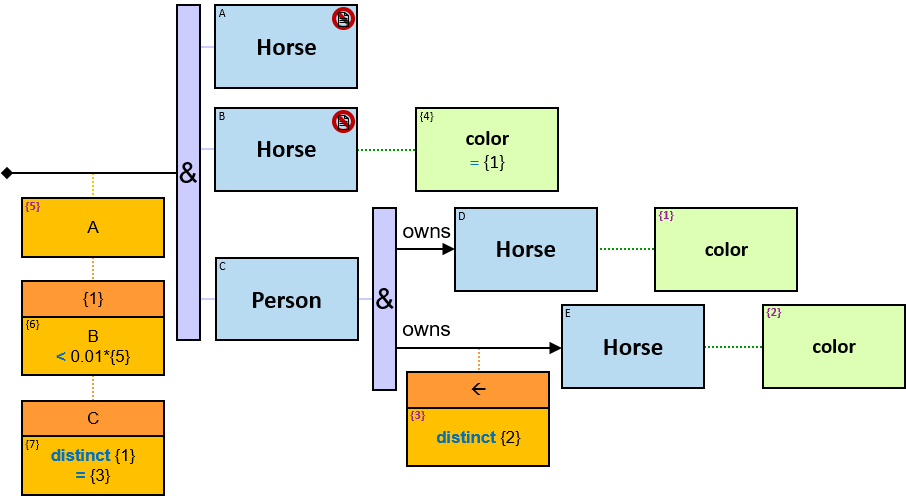
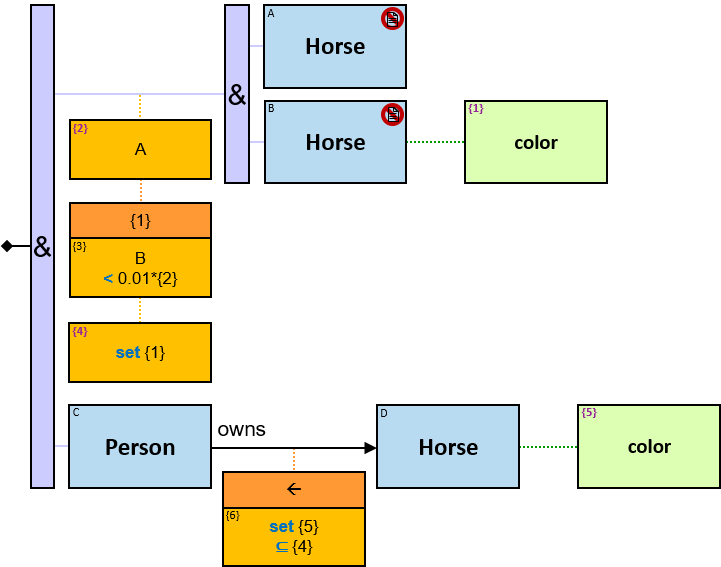
Q338: Any person who owns at least ten horses, at least half of which are of rare colors. A rare color is a color of less than 1% of the horses (two versions)

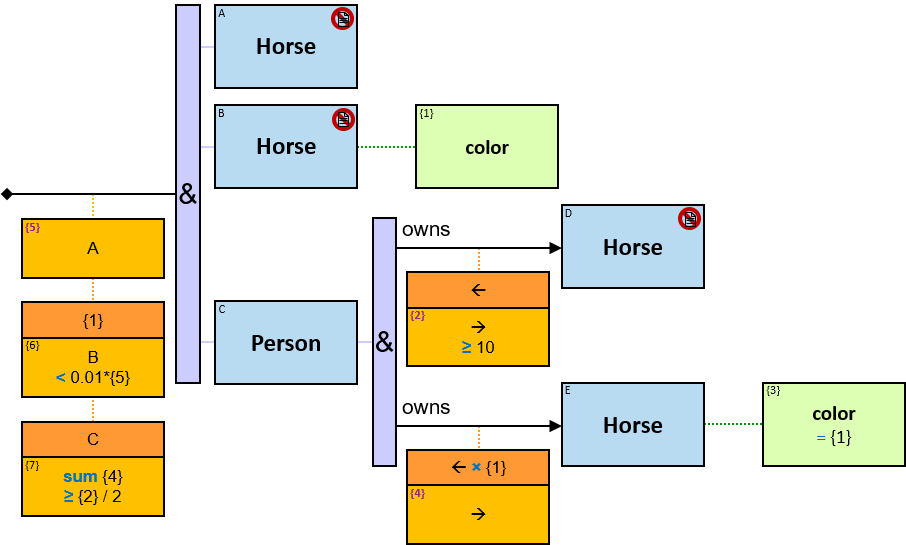
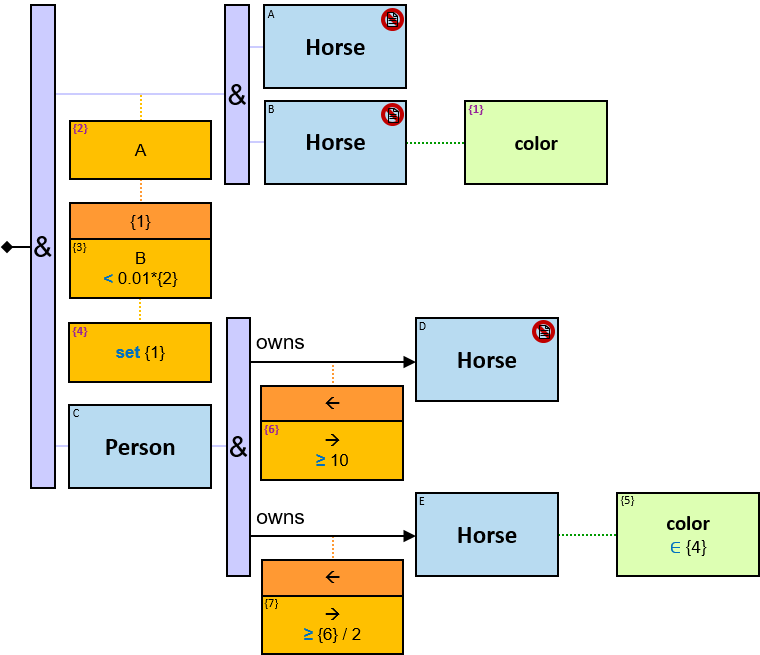
Extended A2 Aggregator

Q330: Any day during which more than five horse-ownerships started

Q270: Any person A and A’s horses of the colors for which there are more than five horse-ownerships by a person

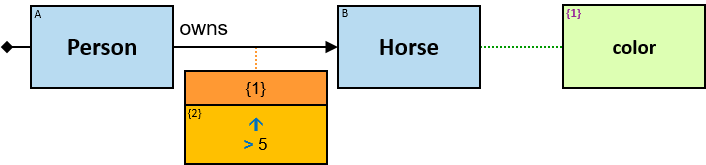
Extended A3 Aggregator

Q331: Any day at which the horse ownerships that started (and ended since) lasted on average for at least ten years

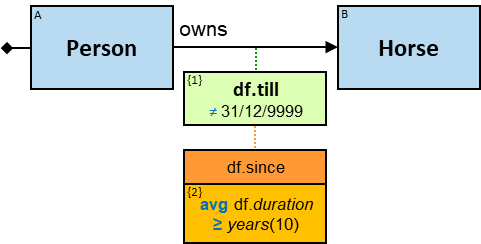
Q271: Any person A and A’s horses of the colors for which the average ownership start date is at least January 1, 1010

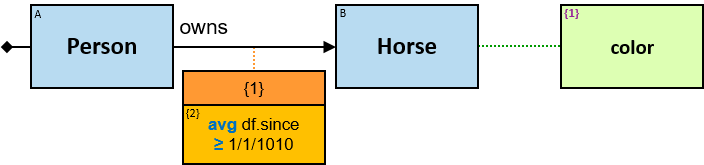
Q263: Any horse of each color of which the average horses’ weight is greater than 450 Kg

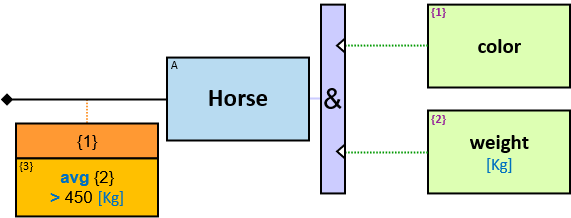
Q265: Any horse of each color of which the average horses’ owners’ height is at least 180 cm

Q155: Any dragon that in each of at least 11 days - froze dragons for more than 100 minutes cumulatively

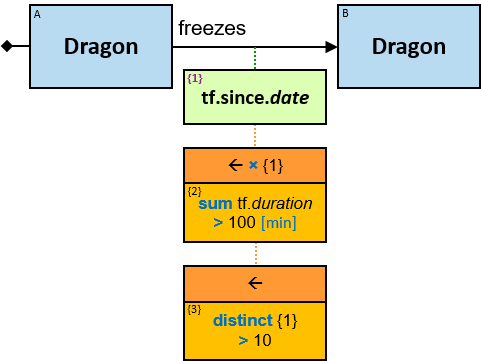
Q156: Any dragon that froze dragon for more than 1000 minutes cumulatively - in the days it froze dragons for more than 100 minutes

Q154: Any dragon that in each of at least four years - in each of at least 11 days - froze between one and five dragons

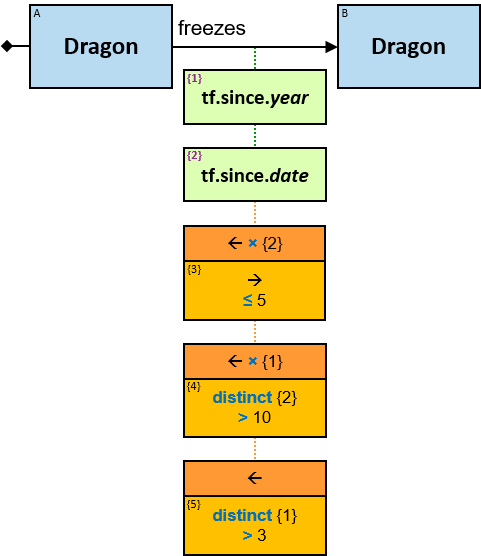
Q159: Any dragon for which there are more days where (it froze/was frozen at least five times, and the number of dragons it froze is greater than the number of dragons that froze it) than days where (it froze/was frozen at least five times, and the number of dragons that froze it is greater than the number of dragons it froze)

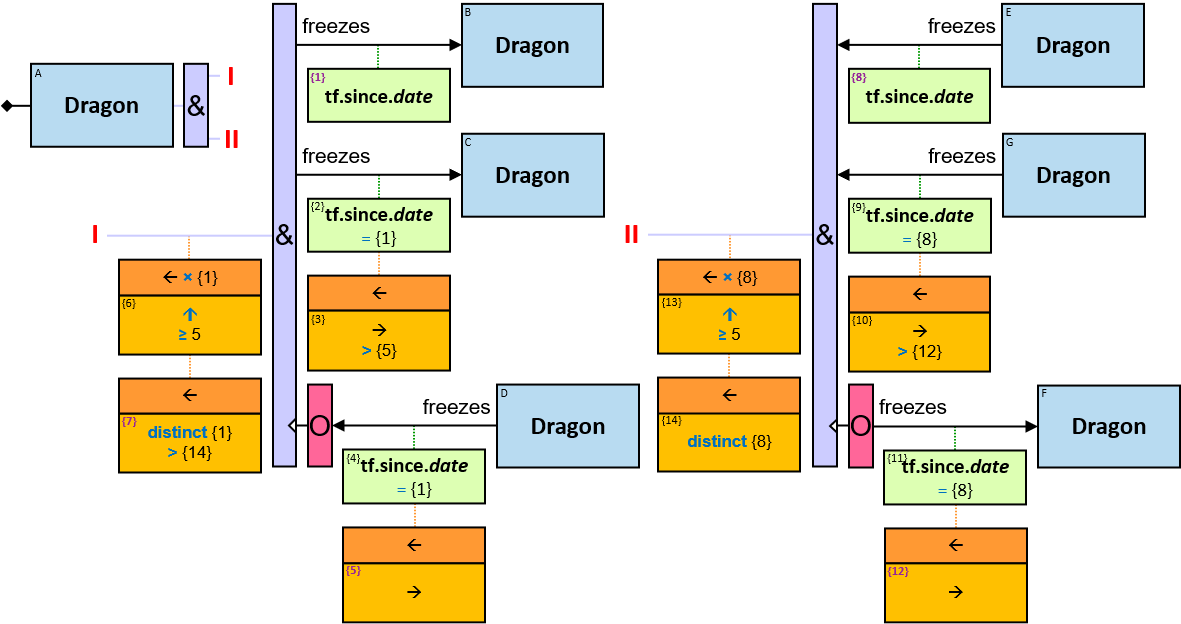
(Compare with Q260)

Q361: Any person A who owns horses of at least five colors, and the sets of weights of A’s horses of each of these colors are identical

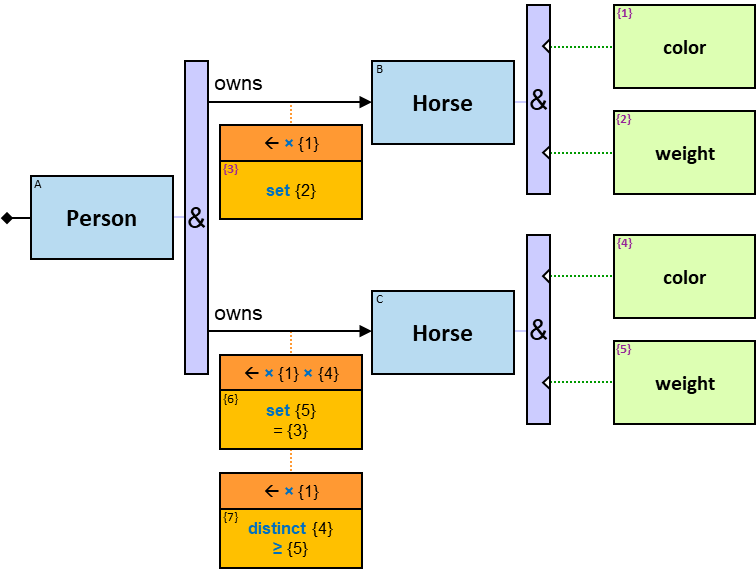
Q320: Any person A where there are more horses of the same colors as A’s owned horses than dragons of the same colors as A’s owned dragons (version 2)

Q321: Any person A where more horses than dragons have the same name-length as a horse/dragon A owns (version 2)

Extended M1 Aggregator

Q220: Any person A and A’s horses of the three colors of which A owns the largest number of horses

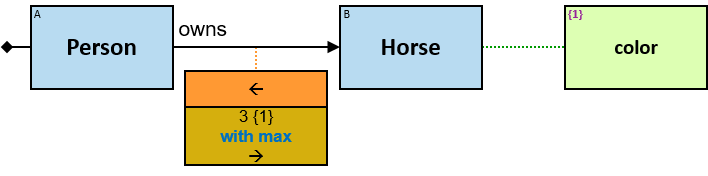
Q262: Any horse of the three most common horse colors

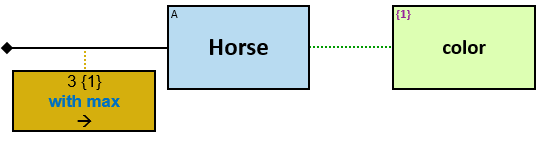
Q224: Any person A and A’s horses of the three colors with the smallest positive number of horse owners (two versions)

Q342: The three colors for which the number of pairs of dragons of that color where at least one of them froze the other - is maximal (version 1)

Note that if a pair of dragons mutually froze each other - we need to count this pair only once.

Q343: The three color-pairs (1, 2) for which the number of dragon pairs where a dragon of color 1 froze a dragon of color 2 is maximal

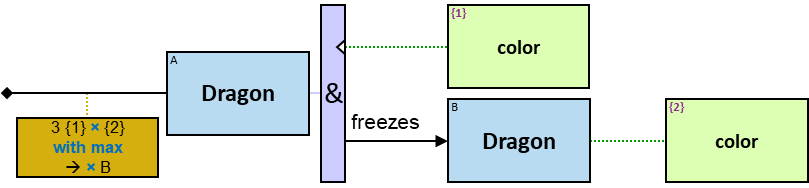
Q251: The three pairs (person, color) with most horses of this color owned by that person

Q211: For each total number of freezes by a dragon: the three dragons that froze the largest number of dragons

Q212: The three most common total number of freezes by a dragon

Q325: For each of the three most common horse colors: the three people who own the largest number of horses of this color

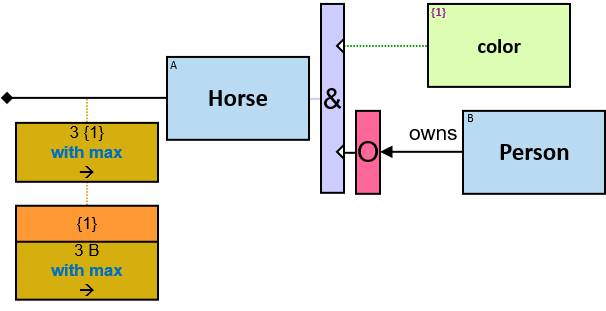
Q326: For the three most common horse colors (combined): the three people who own the largest number of horses of these colors

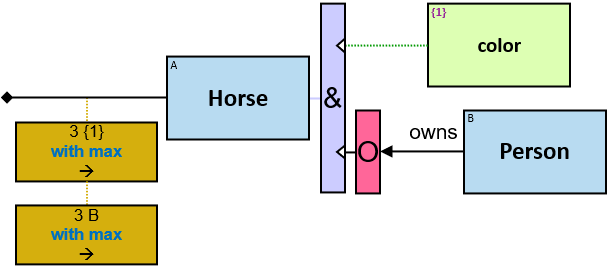
Extended M2 Aggregator

Q215: For each color of dragons that Balerion froze - the three dragons it froze the largest number of times

Q221: Balerion and the dragons it froze - of the three colors it froze dragons the largest number of times

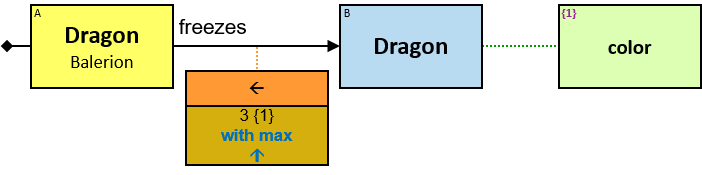
Q280: Any dragon and the dragons it froze - of the three colors it froze dragons the largest number of times

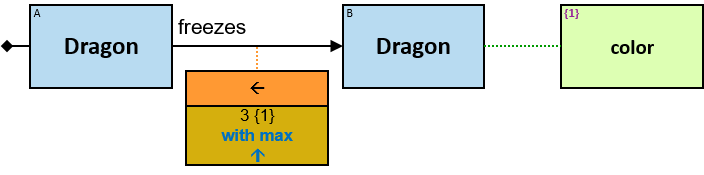
Q253: For each number of dragon’s owners - the three dragons Balerion froze the largest number of times

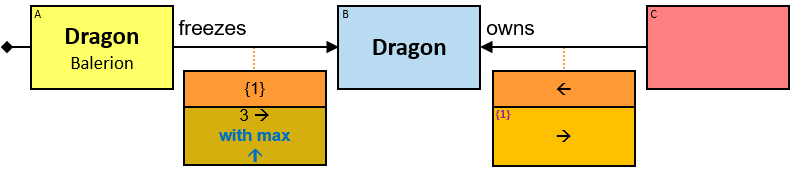
Q225: Any person A and A’s horses of the three colors with the smallest positive number of horse ownerships by a person

Q281: Any dragon and the dragons it froze - of the three colors of which dragons were frozen the largest number of times

Q319: Any dragon and the dragons it froze - of the 4th-6th colors of which dragons were frozen the largest number of times (two versions)

Q282: Balerion and the dragons it froze - of the three colors of which dragons were frozen the largest number of times

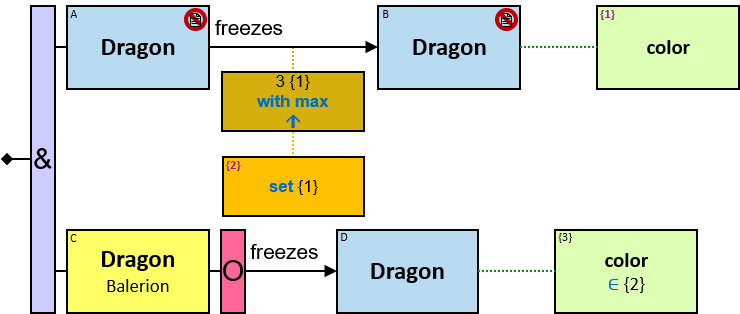
Q209: The three most owned entity-types

Q210: The three pairs (owner entity-type, owned entity-type) with most _owns relationships_

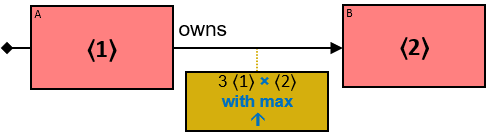
Q369: The three most common relationship-types and the number of relationships of each of these types

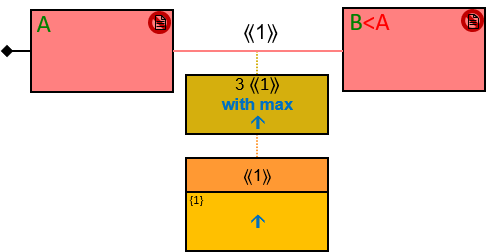
Q370: The most common relationship-type between entities of the same type

Extended M3 Aggregator

Q275: Any person A and A’s horses of the three colors of which A owns the heaviest horse

Even if A’s three heaviest horses are of the same color, we would still get all A’s horses for two more colors (those with the next heaviest horses)

Q223: Any person A and A’s horses of the three colors for which the cumulative weight of A’s horses is maximal

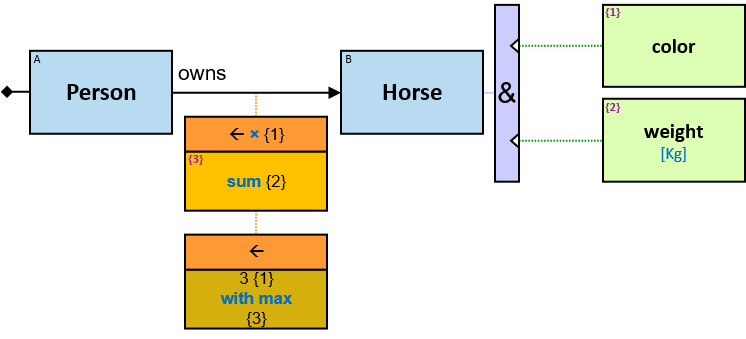
Q222: Any person A and A’s horses of the three colors for which A’s average ownership start date is the latest

Q269: Any person A and A’s horses of the three colors for which the average ownership start date is the latest

Q276: Any person A and A’s horses of the three colors for which the earliest horse ownership start date is the earliest

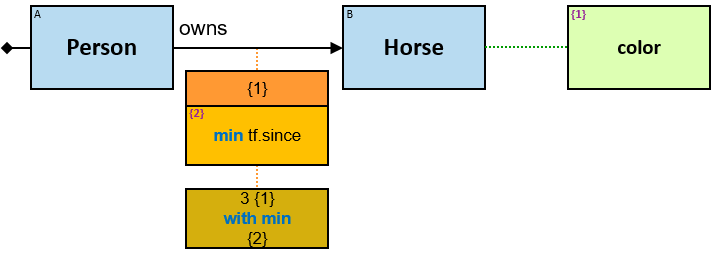
Even if the three horses with the earliest ownership start date are of the same color, we would still get all people and their horses of two more colors (of the next-earliest ownership start dates)

Q216: Any dragon Balerion froze during the three 30-day timeframes during which it froze dragons the largest number of times

Q373: The three 30-day timeframes during which dragons were frozen the largest number of times

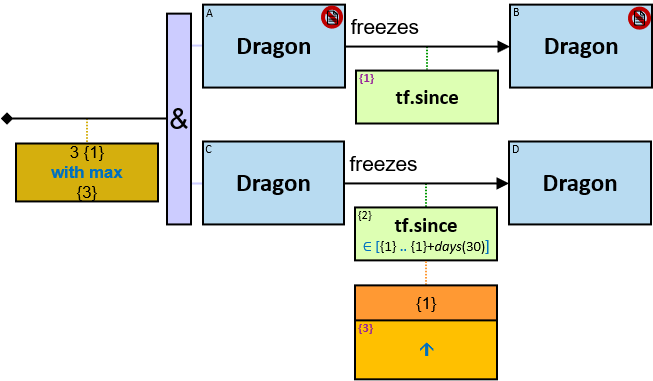
Q374: The three most prolonged timeframes during which no dragon was frozen

Q264: Any horse of the three colors of which the average horses’ weight is maximal

Q226: Any person A and A’s horses - of the three horse-colors for which the average height of the horse owners is minimal

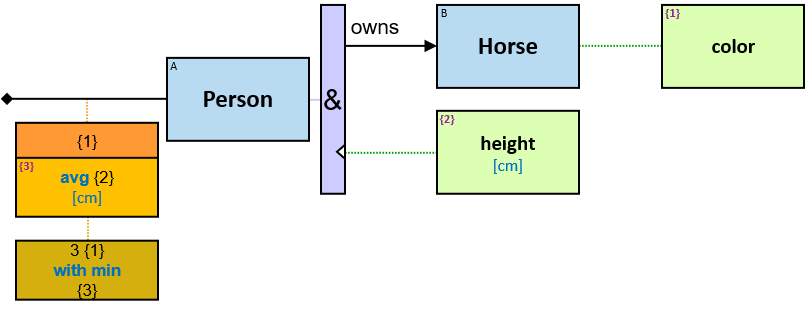
Q342: The three colors for which the number of pairs of dragons of that color where at least one of them froze the other - is maximal (versions 2, 3)

Note that if a pair of dragons mutually froze each other - we need to count this pair only once.

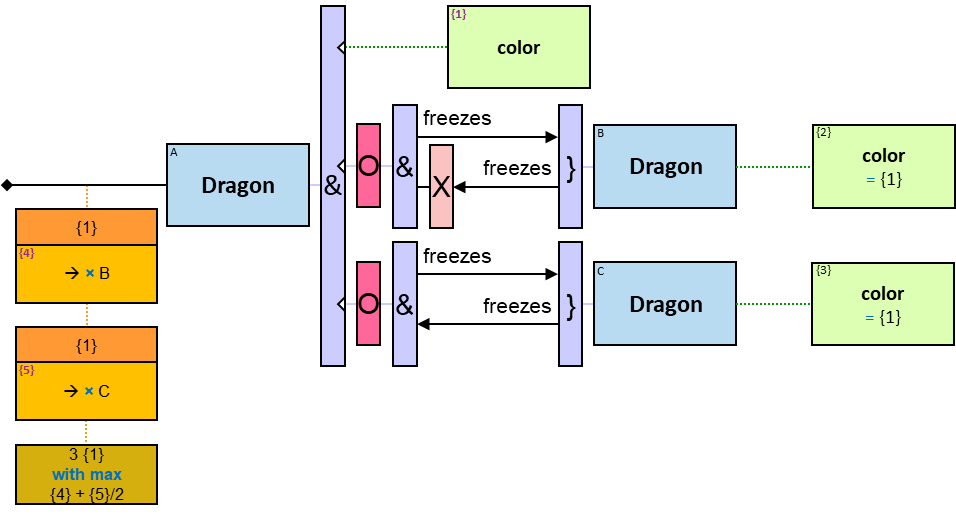
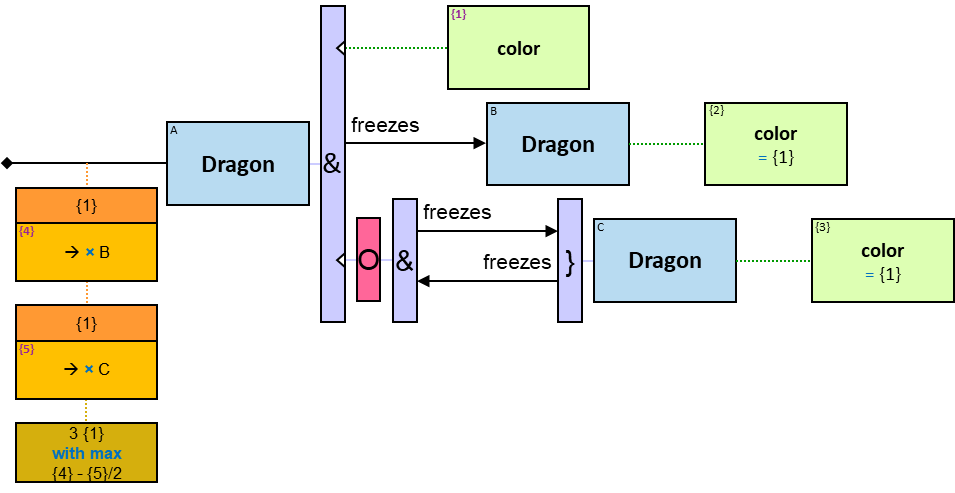
Extended R1 Aggregator

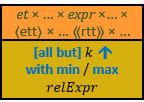
Q273: For each horse color - the three horse-ownerships with the latest ownership start date

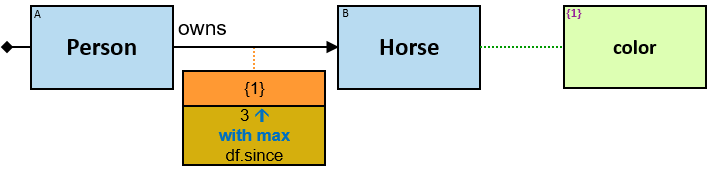
Multivalued Functions and Expressions

A multivalued function is a function that may associate zero or more values to each input. In V1, expressions composed of multivalued functions are evaluated separately for each output associated with the input.

V1 supports the following multivalued functions:

• el: St ⇉ 𝑡 - associates a set with each of its elements
• el: Bt ⇉ 𝑡 - associates a bag with each of its elements
• subset: St ⇉ St - associates a set with each of its nonempty subsets
• subbag: Bt ⇉ Bt - associates a bag with each of its nonempty subbags

All these multivalued functions have no associations when the input is an empty set or bag.

In the following examples, Person has the following property: nicknames: set(string).

Q379: Any person who has at least one nickname

Even though {1} has no explicit constraints, it must have at least one assignment.

Q307: Any person who has a nickname containing an ‘a’

{1} is a multivalued expression. For each person, {1} is evaluated for each nickname. If at least one nickname satisfies the constraint - this person is a valid assignment.

Q316: Any pair of people with a common nickname

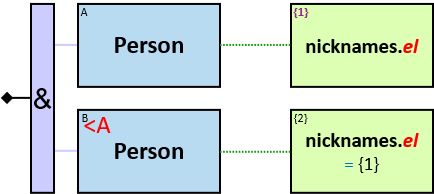
{1} is evaluated for each non-null nickname of A. {2} is evaluated for each non-null nickname of B. All combinations are evaluated.

Q308: Any person who has a nickname containing both (an ‘a’ or an ‘A’) and (a ‘b’ or a ‘B’)

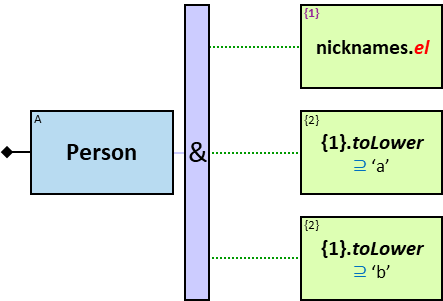
For each person, {1} is evaluated for each non-null nickname. {2} and {3} are evaluated for each value of {1}. If {2} and {3} satisfies the constraints for at least one evaluation of {1} - the person is a valid assignment. A person with no non-null nicknames will not be evaluated.

Q309: Any person who has at least two nicknames (two versions)

The count function returns the number of values a multivalued expression has. {1} is a single-valued expression.

An A3 aggregator can be used for aggregating the evaluations of a multivalued expression:

• The aggregator appears below an All quantifier-input
• The per clause is ‘←’
• There are only entity’s expressions right of the quantifier
• There is exactly one multivalued expression right of the quantifier

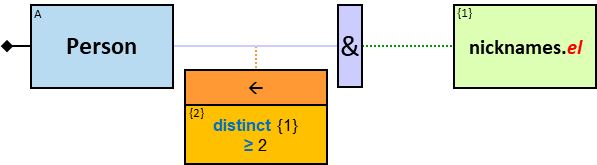
{2} is assigned with the number of distinct non-null evaluations of {1}.

Q310: Any person who has at least two nicknames - each contains an ‘a’ (two versions)

Q311: Any person who has at least five nicknames - each contains either an ‘a’ or a ‘b’

Q312: Any person with more nicknames containing a ‘b’ or a ‘B’ than nicknames containing an ‘a’ or an ‘A’

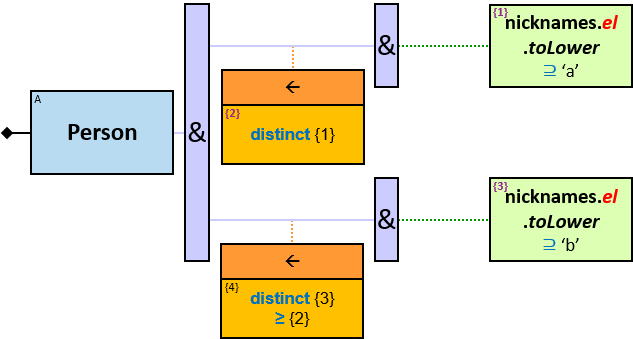
Note that if a nickname contains both an ‘a’ and a ‘b’ - it would be assigned to both {1} and {4}.

Q313: Any person A that has at least one nickname and all A’s nicknames contain an ‘a’

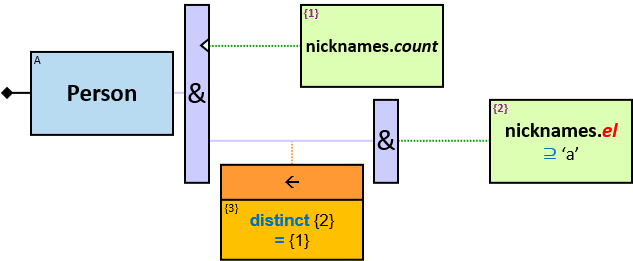
Q314: Any person who has at least one nickname, but none of its nicknames contain an ‘a’

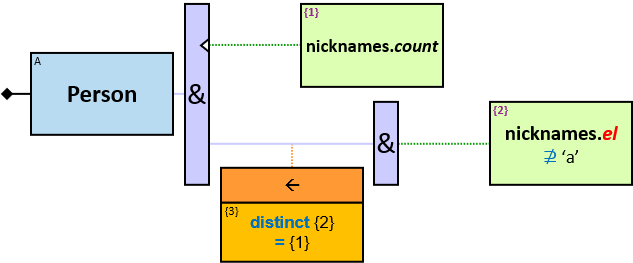
Q315: Any person A that the average length of A’s three shortest nicknames is at least three

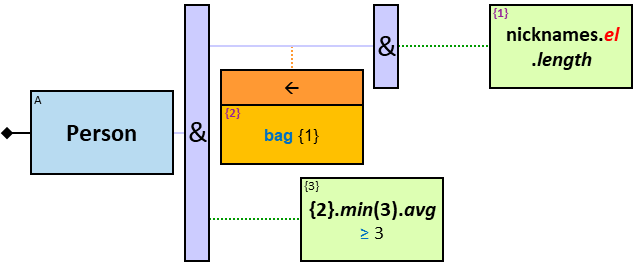
Q348: Any person A that the combined weight of three, four or five of A’s horses - is exactly 1000 Kg

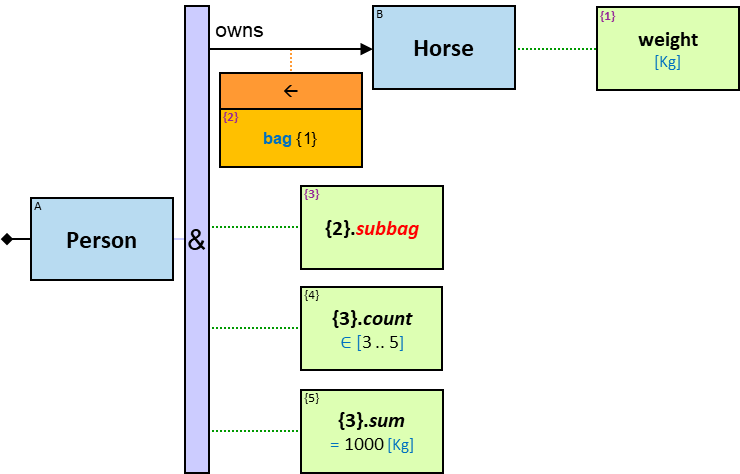
Q349: Any person A that A’s horses can be split into three groups with an identical combined weight

Relationships may have multivalued expressions as well.

Q284: Any person who owned the same five horses - for at least ten consecutive days (version 2)

The set function returns a set of all individual dates within the tf dateframe. el is a single element of this set (a single date). Each value is evaluated separately.

Q340: Any person who owned the same five horses - in at least ten (not necessarily consecutive) days

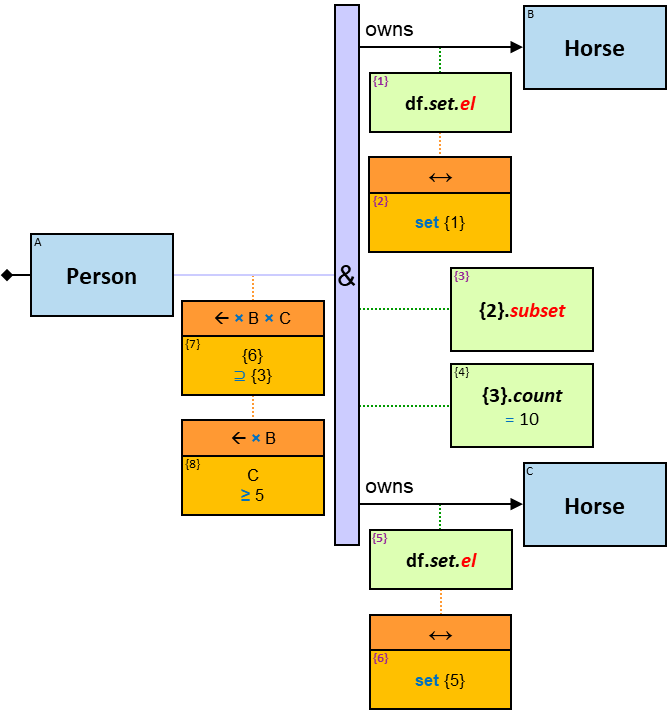
{2} and {5} are sets of all horse ownership dates, aggregated over all ‘owns’ relationships.

Expression-tag {3} represents one subset of set expression {2}. The constraint in {4} limits assignments to {3} to subsets of {2} with exactly ten elements. {2}, {3} and {4} are properties of A × B.

Q287: Any person who at each day of at least ten (not necessarily consecutive) days - owned the same two horses

Q327: Any person who at each day of at least ten consecutive days - owned at least five horses (not necessarily the same horses each day)

Q318: Any dragon Balerion froze/fired at during the three 30-day timeframes during which it froze/fired at dragons the largest number of times

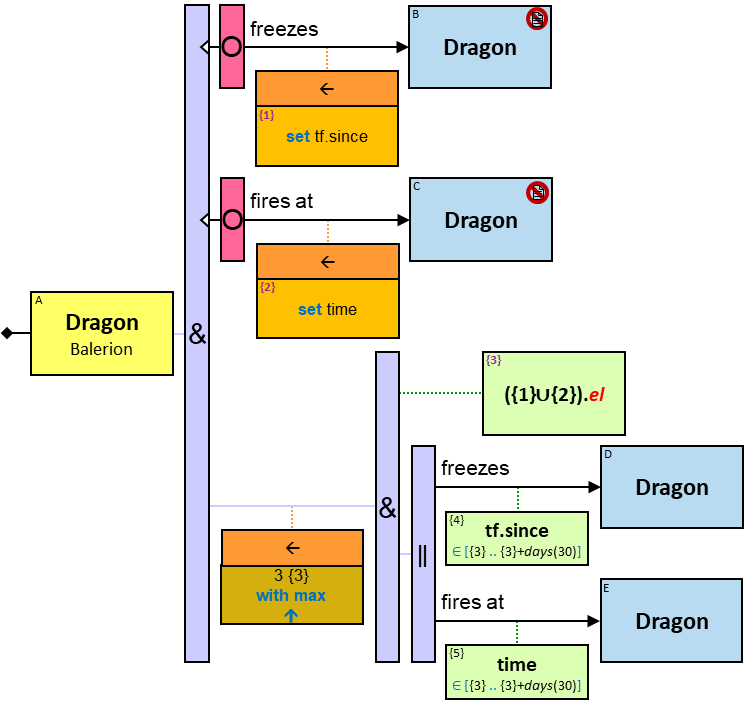
Note that {1} and {2} are defined right of an ‘O’, hence evaluated to empty sets when the optional parts have no assignments. Since 𝑆 ∪ ∅ = 𝑆, the pattern is valid even if Balerion froze no dragon or if it fired at no dragon.

{3} is a property of A, but, being an aggregated multivalued expression, must be defined right of the aggregator.

Q371: Any dragon Balerion froze/fired at during the three non-overlapping 30-day timeframes during which it froze/fired at dragons the largest number of times

{1}, {2} and {3} are sets of intervals of datetimeframe. In {5}, {3} is coerced to set of datetimeframes. {4} and {5} limit assignment to {3} to sets with three non-overlapping members.

{6} is a multivalued expression evaluated per each value of the multivalued expression {3}. The M2 aggregator is evaluated for all assignments to {6} of each assignment to {3}.

Application: Spatiotemporality

Dragon-spotting is a major hobby around the world. Dragon-spotters document the time, location, and of course - the identity of the dragon they spotted. The location may be a point (longitude and latitude) or a small area - when they are not sure about the exact coordinates. Most observations are attributed to the spotter, but in many ancient documents - the dragon-spotter is unknown.

We will extend our sample schema with the following relationship-type:

• spotted: {(Person, Dragon), (Null, Dragon)} - time: datetime, loc: location

spotted is a relationship between a dragon-spotter (which may be unknown) and the dragon spotted. The properties of the relationship are the time and the location where the dragon was spotted.

location is an opaque data type (see above) that contains a geographic point (e.g., latitude and longitude) or a geographic shape (a circle, an ellipse, a polygon, etc.)

Functions over location expressions:

• dist(location, location) → float - the distance [Km] between these two locations

Constraint operators over location expressions:

• ⊃ 𝑙, ⊇ 𝑙, ⊅ 𝑙, ⊉ 𝑙 - [not] [proper] superspace of 𝑙
• ⊂ 𝑙, ⊆ 𝑙, ⊄ 𝑙, ⊈ 𝑙 - [not] [proper] subspace of 𝑙

Two entity-types are defined as well:

• Landmark - loc: location
• City - loc: location

Note that we chose to hold the location of stationary entities (landmark, city) as entity properties, and hold the location of mobile entities (dragon) as relationship properties.

G1: Any dragon observed at Dragonmont Peak

G2: Any dragon observed within 5 Km from Dragonmont Peak

G3: Any dragon observed within 5 Km from Dragonmont Peak at least five times during a 7-day period

G4: Any dragon observed within 5 Km from Dragonmont Peak between 4 AM and 7 AM in at least five days during a 7-day period

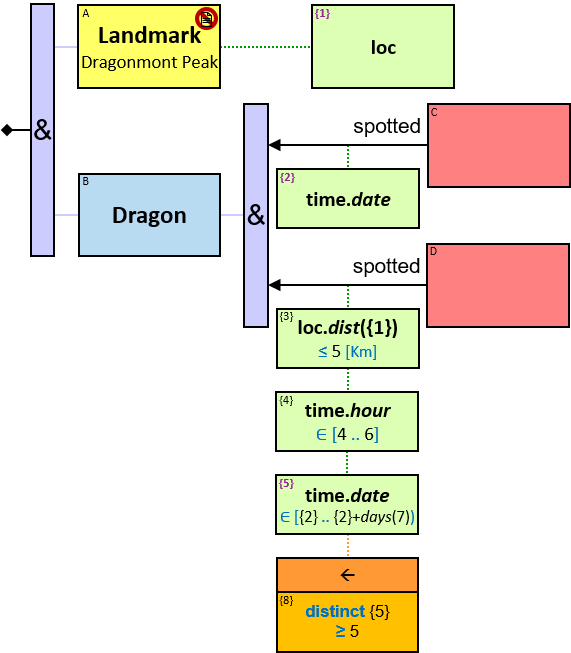
G5: Any dragon observed within 5 Km from Dragonmont Peak in at least five separate weeks

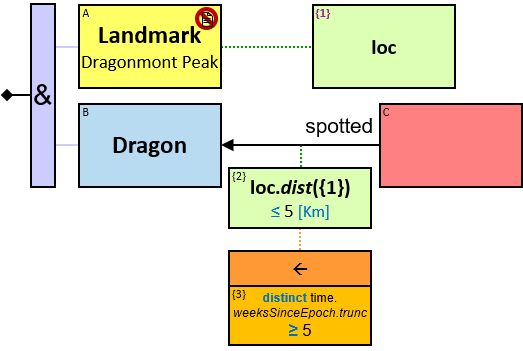
G6: Any week during which at least five dragons were observed within 5 Km from Dragonmont Peak

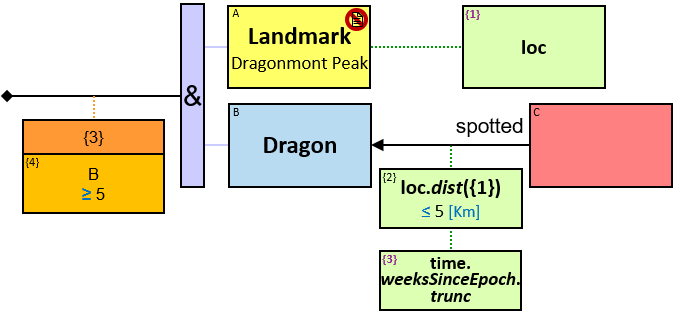
G7: Any dragon with conflicting observations (given that dragons cannot fly faster than 300 Km/h)

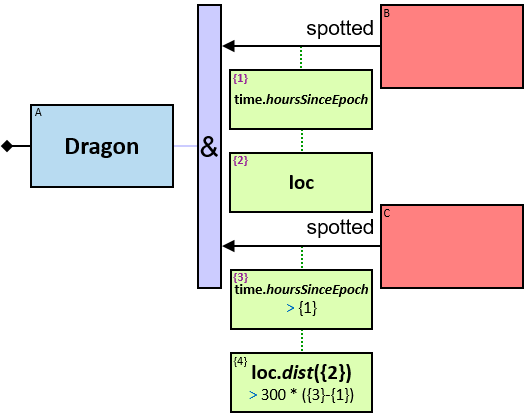
G8: Any Sarnorian B for whom at least three of B’s dragons were spotted within 5 Km from Dragonmont Peak - in a timeframe of 24 hours

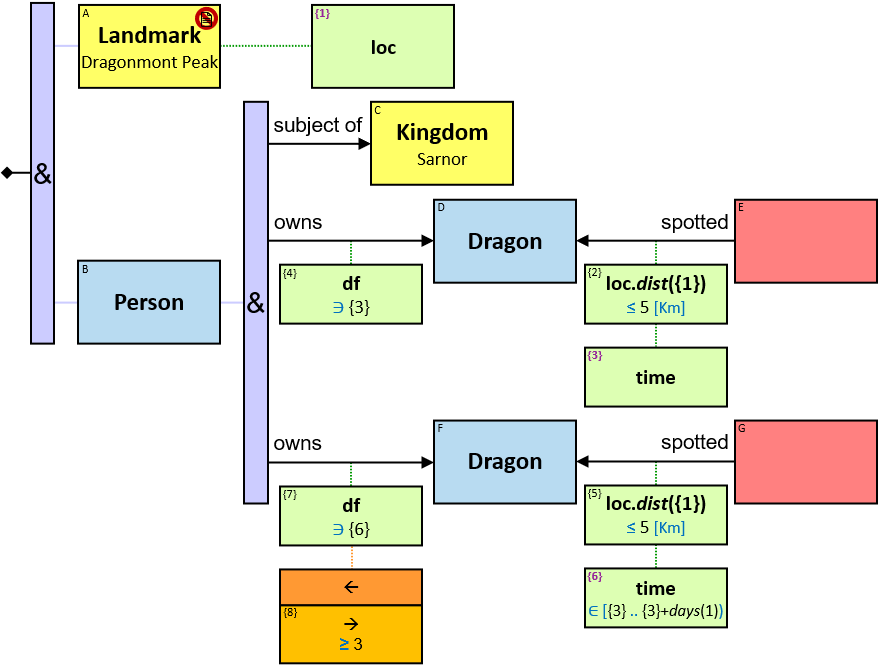
G9: Any dragon that stayed within 5 Km from Dragonmont Peak for at least one week (To ensure this - the dragon should have been spotted there at least once per 6 hours and not spotted at any other location throughout that period)

G10: Any pair of dragons that were spotted within 5 Km from each other at least five observation-pairs (To ensure this - paired observation should differ in up to 5 minutes; observation pairs should differ in at least 24 hours)

G11: Any pair of dragons A and B, where at least ten times in the last 300 days A was spotted at a distance of less than 1 Km from places where B was spotted between one day and five days before

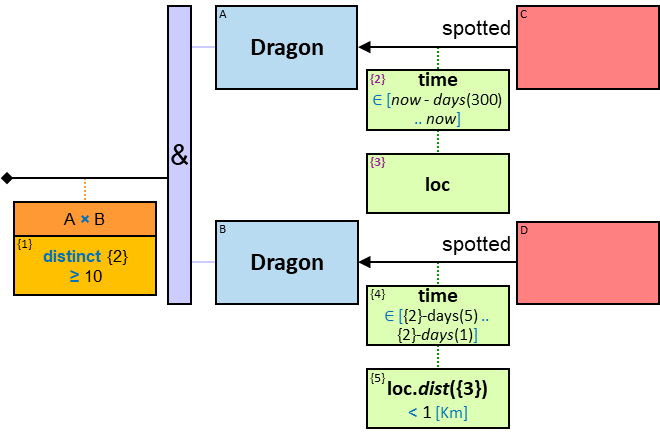
G12: Any pair of dragons that were spotted within 5 Km from each other at least 5 observation-pairs during a 30-day period (To ensure this - paired observation should differ in up to 5 minutes; observation pairs should differ in at least 24 hours)

G13: Any Sarnorian E whose dragons seem to “spy” on Balerion (at least one of E’s dragons was spotted at most 1 Km from Balerion throughout a ten-day period. Paired observation should differ in up to 5 minutes; observation pairs should differ in no more than 1 hour)

G14: Any pair of dragons that were spotted not less than 1000 Km from each other throughout a period of at least one year (To ensure this - paired observation should differ in up to 30 minutes; observation pairs should differ in no more than 24 hours)

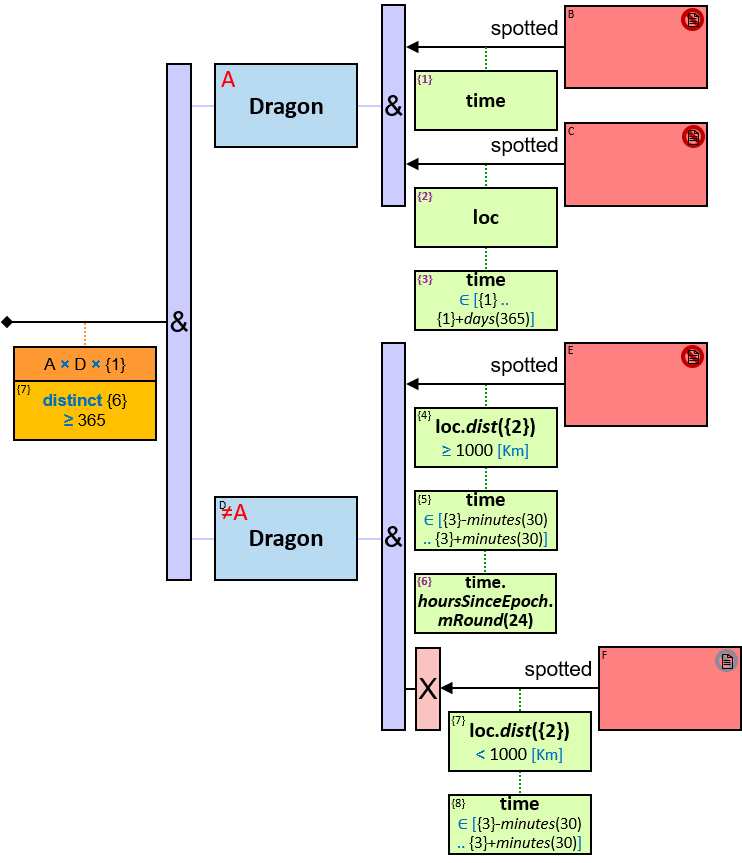
G15: Any landmark where at least five dragons were spotted within 5 Km from it

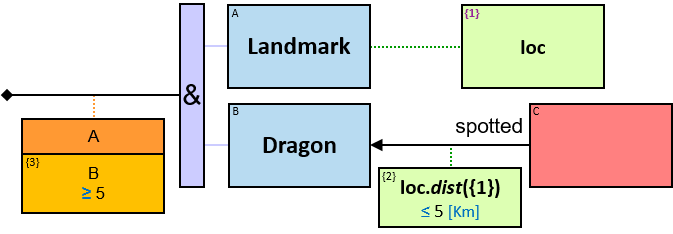
G16: Any city in which at least five dragons were spotted throughout a 2-minutes period

G17: Any landmark where at least five dragons were spotted within 5 Km from it throughout a 7-day period

G18: Any dragon spotted in at least ten cities

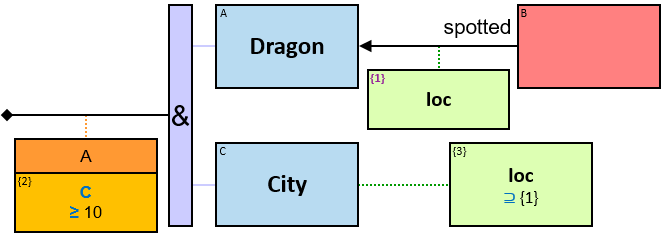
G19: Any dragon spotted in at least ten cities throughout a ten-day period

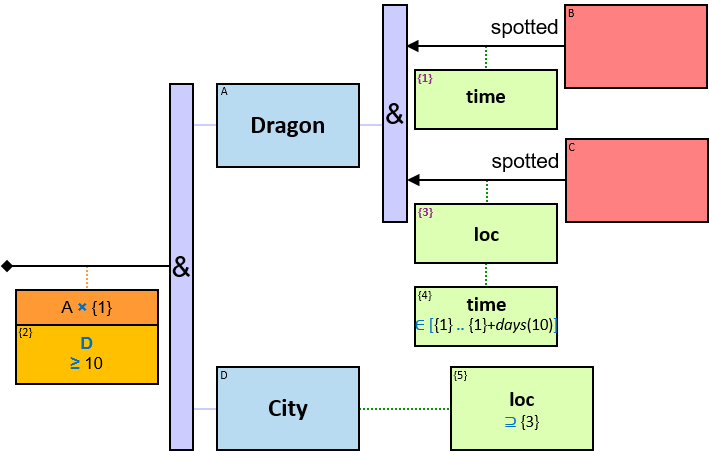
G20: Any dragon that traveled at least 2000 Km in a 24-hours period

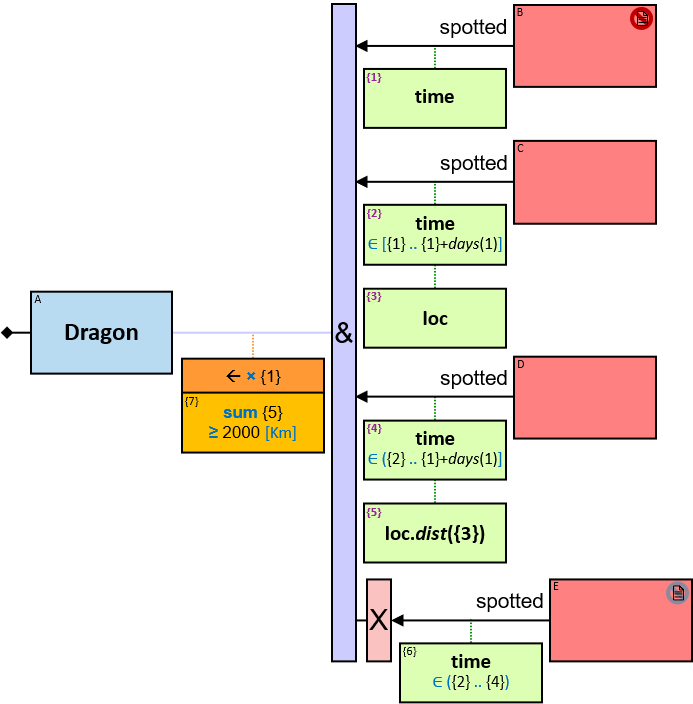
G21: Any dragon-spotter that spotted the same dragon at two locations - at least 1000 Km apart